
Положение, о котором идет речь, иллюстрируется фиг. 11.6.

Фиг. 11.6. Волны в одномерной решетке а одним «примесным» атомом в n= 0.
Используя формулы (11.32) для а -1и а +1, можно из средней тройки уравнений (11.28) найти а 0и два коэффициента b и g. Таким образом, мы найдем полное решение. Надо решить три уравнения (полагая x n =nb) :

Вспомните, что (11.30) выражает E через k . Подставьте это значение Е в уравнения и учтите, что

тогда из первого уравнения получится
a 0=1+b, (11.34)
а из третьего
a 0=g, (11.35)
что согласуется друг с другом только тогда, когда
g=1+b. (11.36)
Это уравнение сообщает нам, что прошедшая волна (g) — это просто исходная падающая волна (1) плюс добавочная волна (b), равная отраженной. Это не всегда так, но при рассеянии на одном только атоме оказывается, что это так. Если бы у вас была целая группа атомов примеси, то величина, добавляемая к волне, бегущей вперед, не обязательно вышла бы такой же, как у отраженной волны.
Амплитуду b отраженной волны мы можем получить из среднего из уравнений (11.33); окажется, что

Мы получили полное решение для решетки с одним необычным
атомом.
Вас могло удивить, отчего это проходящая волна оказалась «выше», чем падавшая, если судить по уравнению (11.34). Но вспомните, что b и g — числа комплексные и что число частиц в волне (или, лучше сказать, вероятность обнаружить частицу) пропорционально квадрату модуля амплитуды. В действительности «сохранение числа электронов» будет выполнено лишь при условии
|b| 2+|g| 2=1. (11.38)
Попробуйте показать, что в нашем решении так оно и есть.
§ 7. Захват нерегулярностями решетки
Бывает и другой интересный случай. Он может возникнуть, когда F число отрицательное. Если энергия электрона в атоме примеси (при n= 0) ниже, чем где-либо в другом месте, то электрон может оказаться захваченным этим атомом. Иначе говоря, если Е 0+ F ниже самого низа полосы (меньше, чем Е 0 - 2 А), тогда электрон может оказаться «пойманным» в состояние с Е<���Е 0 - 2 А. Из всего того, что мы делали до сих пор, такое решение не могло получиться. Но это решение можно получить, если в пробном решении (11.15) разрешить k принимать мнимые значения. Положим k = ix. Для n <0 и для n >0 у нас опять будут разные решения. Для n >0 допустимое решение могло бы иметь вид
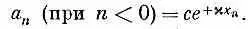
В экспоненте мы выбрали плюс; иначе амплитуда при больших отрицательных n стала бы бесконечно большой. Точно так же допустимое решение для n >0 имело бы вид
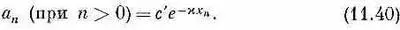
Если подставить эти пробные решения в (11.28), то они удовлетворят всем уравнениям, кроме средней тройки, при условии, что

А раз сумма этих двух экспонент всегда больше 2, то эта энергия оказывается за пределами (ниже) обычной полосы. Это-то мы и искали. Оставшейся тройке уравнений (11.28) удастся удовлетворить, если взять с = с' и если к выбрать так, чтобы
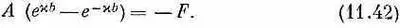
Сопоставив это уравнение с (11.41), найдем энергию захваченного электрона

Захваченный электрон обладает одной-единственной энергией (а не целой полосой); она расположена несколько ниже полосы проводимости.
Заметьте, что амплитуды (11.39) и (11.40) не утверждают, что пойманный электрон сидит прямо в атоме примеси. Вероятность обнаружить его у одного из соседних атомов дается квадратом этих амплитуд. Изменение ее показано столбиками на фиг. 11.7 (при каком-то наборе параметров).
Читать дальше






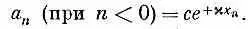
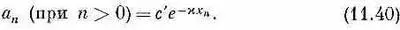

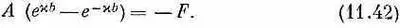




![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)

![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)


