Чтобы облегчить подобные рассуждения, мы сейчас придумаем сокращенное изображение наших усовершенствованных приборов Штерна — Герлаха. Вместо каждого такого прибора мы будем ставить символ

(Этот символ вы не встретите в квантовой механике; мы попросту выдумали его для этой главы. Он означает просто сокращенное изображение прибора, показанного на фиг. 3.3.) Поскольку мы I собираемся пользоваться несколькими приборами одновременно, имеющими к тому же разную ориентацию, то каждый из них мы будем отмечать буквой внизу. Так, символ (3.1) обозначает прибор S. Загораживая внутри один или больше пучков, мы будем отмечать это вертикальными чертами, показывающими, какой из пучков перекрыт, наподобие

Различные мыслимые комбинации собраны на фиг. 3.5.
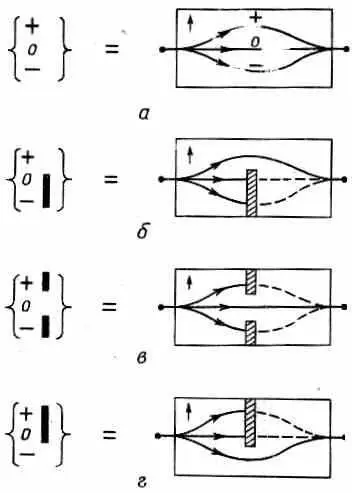
Фиг. 3.5. Специальные сокращенные обозначения для фильтров типа Штерна — Герлаха.
Если два фильтра стоят друг за другом (как на фиг. 3.4), мы и символы будем ставить друг за другом:
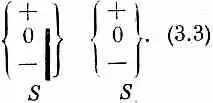
При таком расположении все, что прошло через первый фильтр, пройдет и через второй. В самом деле, даже если мы перекроем каналы «нуль» и «минус» второго прибора, так что будет

все равно прохождение через второй прибор будет 100%-ным. Но если имеется
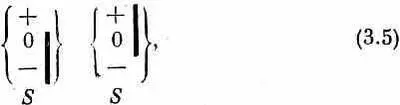
то из дальнего конца не выйдет ничего. Равным образом ничего не выйдет и при
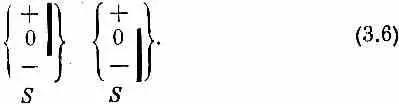
С другой стороны,
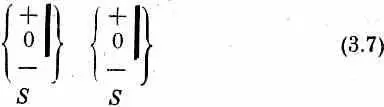
было бы просто эквивалентно одному только
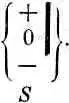
Теперь мы хотим описать эти опыты квантовомеханически. Мы скажем, что атом находится в состоянии (+ S ), если он прошел через прибор, изображенный на фиг, 3.5, б , что он находится в состоянии (0S), если прошёл сквозь прибор на фиг. 3.5, в, и что он находится в состоянии (- S), если прошел сквозь прибор на фиг. 3.5, г. Затем пусть < b|a > будет амплитуда того, что атом, который находится в состояний а, пройдя через прибор, окажется в состоянии b . Можно сказать < b | а > есть амплитуда для атома в состоянии а перейти в состояние b. Опыт (3.4) означает, что
<+ S |+ S >=1,
а (3.5) — что
<-S|+S>=0.
Точно так же и результат (3.6) означает, что
<+ S |- S >=0,
а (3.7)— что
<- S |- S >=1.
Пока мы имеем дело только с «чистыми» состояниями, т. е. пока бывает открыт только один канал, таких амплитуд — всего девять. Их можно перечислить в следующей таблице:

Эта совокупность девяти чисел, именуемая матрицей, подытоживает описанные нами явления.
§ 2. Опыты с профильтрованными атомами
Теперь возникает важный вопрос: что будет, если второй
прибор наклонить под некоторым углом, так чтобы ось его поля больше не была параллельной оси первого? Его можно не только наклонить, но и направить в другую сторону, например повернуть пучок поперек. Вначале для простоты возьмем такое расположение, при котором второй прибор Штерна — Герлаха повернут вокруг оси у на угол а (фиг. 3.6).
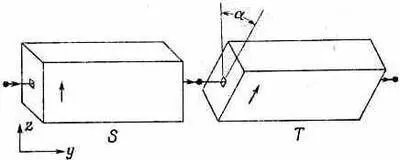
Фиг. 3.6. Два последовательно соединенных фильтра типа Штерна — Герлаха.
Второй повернут, относительно первого на угол a .
Такой прибор мы обозначим буквой Т. Пусть мы теперь предприняли следующий опыт:
Читать дальше






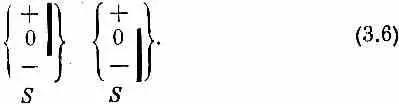
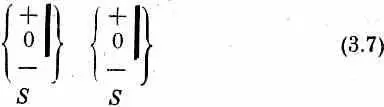
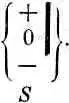





![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)

![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)


