где Dr впоследствии надо будет заменить на d/2. Завершая доказательство так, как это было сделано выше, мы приведем уравнение (6.19) к виду
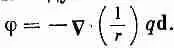
Это то же уравнение, что и (6.16). Надо только заменить qd на р и вставить потерянный по дороге множитель 1/4pe 0. Взглянув на это уравнение по-иному, видим, что дипольный потенциал (6.13) можно толковать как
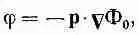
(6.20)
где Ф 0=1/4pe 0r — потенциал единичного точечного заряда.
Хотя потенциал данного распределения зарядов всегда может быть найден при помощи интегрирования, иногда можно сберечь время, применив какой-нибудь хитроумный прием. Например, на помощь часто приходит принцип наложения. Если нам дано распределение зарядов, которое можно составить из двух распределений с уже известными потенциалами, то искомый потенциал легко получить, просто сложив уже известные между собой. Наш вывод формулы (6.20) — один из примеров применения этого приема.
А вот и другой. Пусть имеется сферическая поверхность, на которой поверхностный заряд распределен пропорционально косинусу полярного угла. Интегрировать такое распределение— задача, откровенно говоря, не из приятных. Но как ни странно, на помощь приходит принцип наложения. Представьте себе шар с однородной объемной плотностью положительных зарядов и другой шар с такой же однородной объемной плотностью зарядов, но противоположного знака. Первоначально они вложены друг в друга, образуя нейтральный, т. е. незаряженный шар. Если затем положительный шар чуть сместить по отношению к отрицательному, то нутро незаряженного шара так и останется незаряженным, но на одной стороне возникнет небольшой положительный заряд, а на противоположной — такой же отрицательный (фиг. 6.6). И если относительное смещение двух шаров мало, то эти заряды эквивалентны существованию поверхностного заряда (на сферической поверхности) с плотностью, пропорциональной косинусу полярного угла.
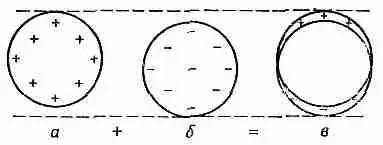
Когда же нам понадобится потенциал этого распределения, то брать интегралы не нужно. Мы знаем, что потенциал каждого заряженного шара —- в точках вне его— совпадает с потенциалом точечного заряда. А два смещенных шара — все равно, что два точечных заряда; значит, искомый потенциал и есть как раз потенциал диполя.
Фиг. 6,6. Две равномерно заряженные сферы, вложенные друг в друга и слегка смещенные, эквивалентны неоднородному распределению
поверхностного заряда.
Таким путем можно показать, что распределение зарядов на сфере радиуса а с поверхностной плотностью
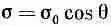
создает снаружи сферы такое же поле, как и диполь с моментом
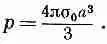
Можно также показать, что внутри сферы поле постоянно и равно
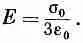
Если q — угол с положительной осью z, то электрическое поле внутри сферы направлено по отрицательной оси z. Рассмотренный нами пример отнюдь не досужая выдумка составителя задач; он нам встретится еще в теории диэлектриков.
§ 5. Дипольное приближение для произвольного распределения
Столь же интересно и не менее важно поле диполя, возникающее при других обстоятельствах. Пусть у нас есть тело со сложным распределением заряда, скажем, как у молекулы воды (см. фиг. 6.2), а нас интересует только поле вдали от него. Мы покажем, что можно получить сравнительно простое выражение для полей, пригодное для расстояний, много больших, чем размеры тела.
Мы можем смотреть на это тело, как на скопление точечных зарядов q i в некоторой ограниченной области (фиг. 6.7). (Позже, если понадобится, мы q i заменим на pdV.) Пускай заряд q i удален от начала координат, выбранного где-то внутри группы зарядов, на расстояние d i . Чему равен потенциал в точке Р, расположенной где-то на отлете, на расстоянии R, много большем, чем самое большое из d i,? Потенциал всего нашего скопления выражается формулой
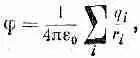
Читать дальше

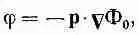

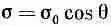
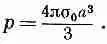
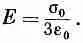
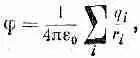




![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)

