С какой скоростью бежит стая волн
В опытах наблюдаются, конечно, не бесконечные синусоидальные волны, а группы или, как сказал бы Рассел, стайки волн. Первые систематические наблюдения групп волн и были сделаны Pacceлом. Он заметил, что скорость перемещения стайки в целом меньше, чем скорость отдельных волн. При наблюдении кажется, что волны продвигаются сквозь группу, как бы исчезая на передней ее границе. Это явление объяснил в 1876 г. Стокс, который и ввел понятие групповой скорости *). Год спустя к этой проблеме вернулся Рэлей. Он нашел, как групповая скорость зависит от дисперсии, и получил формулу, которую мы сейчас выведем.
*) Впервые это понятие для волн в дискретной решетке ввел Гамильтон, рассказавший о своей работе на заседании Ирландской академии в 1839 г. и опубликовавший два кратких сообщения. В его бумагах, найденных и опубликованных 100 лет спустя, содержалась очень подробно разработанная теория групповой скорости таких волн.
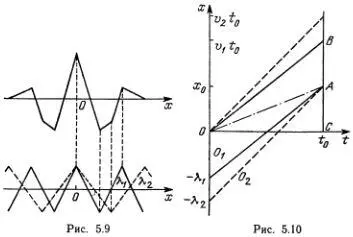
Мы воспроизведем в упрощенном виде рассуждения Рэлея, приведенные в его книге «Теория звука», первой и одной из лучших книг по общей теории колебаний и волн **). Сначала предельно упростим задачу и рассмотрим две волны одинаковой амплитуды, но слегка различной длины, распространяющиеся в одном и том же направлении. Рэлей, естественно, рассматривает синусоидальные волны, а мы для наглядности заменим синусоиды пилообразными волнами. Сумма двух таких волн легко определяется графически, как это сделано на рис. 5.9. Мы видим довольно четко выраженную стайку волн с вершиной А . Если обе волны, из которых образована эта стайка, распространяются с одной и той же скоростью, то вершина, разумеется, бежит с той же скоростью. Предположим теперь, что волны разной длины бегут с разной скоростью, т. е. имеется дисперсия. Пусть, например, v 1= v (λ 1) 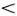 v 2= v (λ 2). Что мы увидим в этом случае? Нарисуем графики движения первой и второй волн (рис. 5.10). Нетрудно понять, что в момент t 0мы снова увидим стайку волн первоначальной формы, но с вершиной в точке x 0. Как видно на рисунке, АВ = λ 1, ВC = v 1 t 0, откуда v 1 t 0- x 0= λ 1. Назовем u = x 0/ t 0групповой скоростью и заметим, что (λ 2- λ 1)/ t 0= v 2- v 1(это тоже ясно видно, из рисунка).
v 2= v (λ 2). Что мы увидим в этом случае? Нарисуем графики движения первой и второй волн (рис. 5.10). Нетрудно понять, что в момент t 0мы снова увидим стайку волн первоначальной формы, но с вершиной в точке x 0. Как видно на рисунке, АВ = λ 1, ВC = v 1 t 0, откуда v 1 t 0- x 0= λ 1. Назовем u = x 0/ t 0групповой скоростью и заметим, что (λ 2- λ 1)/ t 0= v 2- v 1(это тоже ясно видно, из рисунка).
**) Современники Рэлея не сумели вполне оценить, что с появлением этой книги зародилось общее учение о колебаниях и волнах. Даже Гельмгольц, которому книга очень понравилась, считал, что это просто очень хорошая книга по акустике.
Учитывая, что разности длин волн, Δλ = λ 2- λ 1, и разности скоростей, Δ v = v 2- v 1, малы, легко понять, что
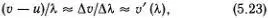
где мы заменили v 1и λ 1на среднюю скорость v = ½( v 1+ v 2) и среднюю длину волны λ = ½(λ 1+ λ 2). Это и есть соотношение Рэлея, связывающее групповую скорость со скоростью гармонической волны (последнюю обычно называют фазовой скоростью ). Смысл этой простой формулы состоит в том, что скорость группы, в которой средняя длина волн входящих в нее гармоник близка к λ, определяется производной фазовой скорости v (λ) по λ при значении λ, равном средней длине волны группы.
Групповую скорость легко определять по графику функции v (λ) (рис. 5.8). Пусть средняя длина волны группы равна λ 2. Проведем из точки O 2касательную до пересечения с осью у . Точка пересечения и дает групповую скорость, которая в этом случае меньше фазовой. Упражнение: докажите, что при λ 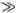 λ миниз формул (5.22) и (5.23) следует, что u
λ миниз формул (5.22) и (5.23) следует, что u  v /2. Попробуйте проверить это соотношение наблюдениями. Точно такое построение можно выполнить и для длин волн, меньших λ мин. При λ = λ минфазовая и групповая скорости, как видно из рисунка, совпадают.
v /2. Попробуйте проверить это соотношение наблюдениями. Точно такое построение можно выполнить и для длин волн, меньших λ мин. При λ = λ минфазовая и групповая скорости, как видно из рисунка, совпадают.
Нетрудно убедиться, что для изученных нами волн на воде групповая скорость u всегда положительна, т. е. группы бегут в ту же сторону, что и волны. Однако если наклон графика v (λ) достаточно большой, то групповая скорость могла бы стать отрицательной. В этом нет ничего сверхъестественного или парадоксального. Просто основная волна длины λ (в радиотехнике ее называют несущей) бежит направо, а вершина огибающей ее кривой, обозначенной на рис. 5.9 штриховой линией (в радиотехнике ее называют модулирующей), бежит налево. Это произойдет, если при λ = λ 2будет выполнено условие tg α 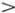 v (λ 2)/λ 2(см. Δ O 2 O ' 2 u (λ 2) на рис. 5.8). Так как tg α = v '(λ 2), то заключаем, что групповая скорость отрицательна, если группа образована волнами со средней длиной, удовлетворяющей условию v '(λ)
v (λ 2)/λ 2(см. Δ O 2 O ' 2 u (λ 2) на рис. 5.8). Так как tg α = v '(λ 2), то заключаем, что групповая скорость отрицательна, если группа образована волнами со средней длиной, удовлетворяющей условию v '(λ) 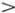 v (λ)/λ.
v (λ)/λ.
Читать дальше

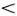 v 2= v (λ 2). Что мы увидим в этом случае? Нарисуем графики движения первой и второй волн (рис. 5.10). Нетрудно понять, что в момент t 0мы снова увидим стайку волн первоначальной формы, но с вершиной в точке x 0. Как видно на рисунке, АВ = λ 1, ВC = v 1 t 0, откуда v 1 t 0- x 0= λ 1. Назовем u = x 0/ t 0групповой скоростью и заметим, что (λ 2- λ 1)/ t 0= v 2- v 1(это тоже ясно видно, из рисунка).
v 2= v (λ 2). Что мы увидим в этом случае? Нарисуем графики движения первой и второй волн (рис. 5.10). Нетрудно понять, что в момент t 0мы снова увидим стайку волн первоначальной формы, но с вершиной в точке x 0. Как видно на рисунке, АВ = λ 1, ВC = v 1 t 0, откуда v 1 t 0- x 0= λ 1. Назовем u = x 0/ t 0групповой скоростью и заметим, что (λ 2- λ 1)/ t 0= v 2- v 1(это тоже ясно видно, из рисунка).
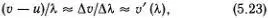
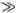 λ миниз формул (5.22) и (5.23) следует, что u
λ миниз формул (5.22) и (5.23) следует, что u  v /2. Попробуйте проверить это соотношение наблюдениями. Точно такое построение можно выполнить и для длин волн, меньших λ мин. При λ = λ минфазовая и групповая скорости, как видно из рисунка, совпадают.
v /2. Попробуйте проверить это соотношение наблюдениями. Точно такое построение можно выполнить и для длин волн, меньших λ мин. При λ = λ минфазовая и групповая скорости, как видно из рисунка, совпадают.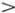 v (λ 2)/λ 2(см. Δ O 2 O ' 2 u (λ 2) на рис. 5.8). Так как tg α = v '(λ 2), то заключаем, что групповая скорость отрицательна, если группа образована волнами со средней длиной, удовлетворяющей условию v '(λ)
v (λ 2)/λ 2(см. Δ O 2 O ' 2 u (λ 2) на рис. 5.8). Так как tg α = v '(λ 2), то заключаем, что групповая скорость отрицательна, если группа образована волнами со средней длиной, удовлетворяющей условию v '(λ) 










