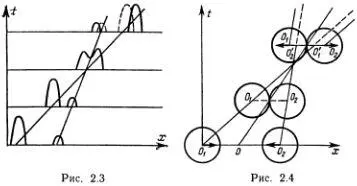
Таким образом, волны вовсе не проходят свободно друг через друга! Они как бы сталкиваются и отталкиваются друг от друга подобно теннисным мячам.
Аналогия с теннисными мячами позволяет понять и только что описанный «сдвиг» уединенных волн при столкновении, который никак нельзя объяснить, если считать, что они свободно проходят друг через друга. Для описания столкновения двух равномерно летящих (без вращения) по одной прямой мячей удобно представить себе сначала их относительное движение (рис. 2.4). Если скорость левого мяча V 1, а скорость правого V 2, то точка О, расположенная посредине между их центрами O 1и O 2, движется с постоянной скоростью V = ½ (V 1+ V 2). Точка О, конечно, представляет собой центр тяжести (точнее, центр масс ) мячей, который сохраняет состояние равномерного прямолинейного движения, если на мячи не действуют внешние силы. Пока мячи не соприкасаются, точка O 1движется относительно точки О со скоростью v = ½ (v 1 - v 2), а O 2— со скоростью - v. В момент соприкосновения t = t 0мячи начинают сминаться, а их центр масс продолжает двигаться со скоростью V. Через небольшой промежуток времени ½ (t' 0 - t 0) относительное движение мячей прекращается, и они начинают отталкиваться друг от друга. Таким образом, в момент ½ (t' 0+ t 0) вся кинетическая энергия относительного движения перешла в потенциальную энергию сжатой резины, и «центры» мячей O 1и O 2движутся в этот момент с одинаковой скоростью V. За время ½ (t' 0- t 0) мячи принимают прежнюю форму. Если пренебречь потерями энергии на разогрев мячей и энергией остаточных колебаний резины, то в момент t' 0 они будут двигаться относительно центра масс О со скоростями - v и v. После удара направление относительного движения просто изменится на противоположное, так что теперь O 1движется со скоростью V - v = v 2, а O 2— со скоростью V + v = v 1.
Итак, мячи не просто обменялись скоростями, но и, сверх того, как ясно видно на рисунке, центр O 2теперь несколько опережает точку O' 1, в которой находился бы первый мяч, если бы столкновения не было, а O 1несколько отстает от O' 2. Такой сдвиг всегда происходит, если время взаимодействия мячей t' 0- t 0достаточно мало. Читатель может сам убедиться, что при достаточно большом времени взаимодействия O 2, наоборот, отстанет от O' 1, а O 1опередит O' 2. Hемного труднее найти то значение времени взаимодействия, при котором O 2совпадает с O' 1, а O 1— c O' 2(о т в е т: 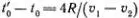 , R — радиус мячей). Интересно также найти O 2 - O' 1 = O' 2- O 1при известных значениях v 1, v 2, t' 0- t 0(о т в е т:
, R — радиус мячей). Интересно также найти O 2 - O' 1 = O' 2- O 1при известных значениях v 1, v 2, t' 0- t 0(о т в е т:  ).
).
Эффект ускорения и отставания становится тем более заметным чем больше размер мячей и меньше их относительная скорость (здесь, конечно, предполагается, что время взаимодействия t' 0- t 0не очень сильно зависит от относительной скорости). Такую же зависимость от относительной скорости можно наблюдать и во взаимодействии уединенных волн. Конечно, она сложнее, так как уединенная волна не имеет резкой границы и отличается от мяча и в других отношениях.
Аналогию можно сделать еще более наглядной, если изображать мячи прямоугольниками, высота которых увеличивается пропорционально кинетической энергии. Тогда их столкновение будет выглядеть совсем похожим на столкновение солитонов. Позже мы познакомимся с другими уединенными волнами, форма которых не зависит от скорости и которые еще больше похожи на частицы.
Почему же все-таки так долго никто не замечал этого самого удивительного свойства уединенной волны? Понятно, что Рассел мог не увидеть этого, хотя, учитывая его необычайную наблюдательность, это тоже как-то надо объяснить. Но ведь уже в 1952 г. была проделана целая серия опытов с уединенными волнами в современном варианте лотка братьев Веберов и с использованием киносъемки. С применением современной техники наблюдение столкновения уединенных волн и обнаружение описанных только что эффектов, казалось бы, не такое трудное дело! По-видимому, объяснение этой удивительной слепоты ученых может быть только одно — все, начиная с Рассела, упорно считали уединенную волну только волной, хотя и довольно необычной.
В какой-то степени в этом повинно и название «уединенная волна», подчеркивающее волновую природу явления. Поэтому когда в 1965 г. американские ученые М. Крускал и Н. Забуски, изучая явления столкновений уединенных волн с помощью электронной вычислительной машины, ясно увидели, что уединенные волны во многом подобны частицам, они немедленно убрали слово «волна», а из «уединенной» (solitary) составили термин «солитон» (soliton), созвучный электрону, протону и другим названиям элементарных частиц *).
Читать дальше


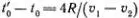 , R — радиус мячей). Интересно также найти O 2 - O' 1 = O' 2- O 1при известных значениях v 1, v 2, t' 0- t 0(о т в е т:
, R — радиус мячей). Интересно также найти O 2 - O' 1 = O' 2- O 1при известных значениях v 1, v 2, t' 0- t 0(о т в е т:  ).
).










