Геннадий Ершов - Как рождается гравитация

2.8.2. Расширение Земли

Ньютон для определения сжатия Земли воспользовался моделью с двумя перпендикулярными сообщающимися скважинами (колодцами), пробуренными через центр Земли: одна – по оси вращения, другая – от экватора, и заполнил их водой. По логике, за счет центробежной силы вода в данных скважинах должна установиться на разных уровнях – в экваториальном колодце уровень воды должен быть выше. Во времена Ньютона не было практических данных измерения, сейчас эти данные есть, но они не согласуются с расчетными.

Приведу один из таких расчетов.

На тело массой m на поверхности Земли действует центробежная сила F c и сила тяжести F g .

M – масса Земли, R – ее радиус.

При этом угловая скорость будет равна:

Найдем отношение F c к F g для шарообразной Земли:

После подстановки значений и вычислений получим:

На экваторе любое тело должно весить примерно на 0,3% меньше, чем на полюсах. В действительности это различие не превышает 0,55% [6].

Можно воспользоваться другим способом вычисления, если приравнять вес каждого элементарного объема вещества на полюсе и на экваторе, при средней плотности Земли (5,52∙10 3 кг/м 3). Иначе, для равновесия на любом расстоянии r от центра Земли будет справедливо соотношение:

Зависимость ускорения свободного падения от радиуса в полярной и экваториальной скважинах одинаково:

где m – масса, заключенная внутри радиуса r .

ρ – плотность вещества, заполняющего скважины.

Если все это подставить в уравнение равновесия (2.14), сократить на m и проинтегрировать по всему радиусу Земли (левую часть – от 0 до полярного радиуса R p , правую – от 0 до экваториального радиуса R e ), то в результате получится соотношение:

Подставив в уравнение (2.16) среднюю плотность Земли 5,52 г/см 3и экваториальный радиус R e =6 378 140 м, получим R p ~6 367 140 м, т. е. полярный радиус должен быть меньше экваториального примерно на 11 км (в действительности – на 21 км), а отношение:

Величина f называется сжатием Земли, в действительности равна 1/298,257

Вычисления дают практически 50-процентное рассогласование с реальными измерениями. Тогда как это объяснить?

Поскольку геофизики не обнаружили никакой дополнительной силы, то находят объяснение в том, что: « Расчет плохо согласуется с реальной формой земной поверхности, поскольку мы не учитывали зависимость плотности от радиуса, а также – отличия реального распределения масс в недрах Земли от сферически-симметричного » [6].

Статистически распределение массы в недрах Земли мало изменится, так как течение жидкой магмы за 4,5 млрд лет уже давно уравновесило чаши весов, поэтому нужно искать другие силы.

2.8.3. Расширение Земли электромагнитными силами

На мой взгляд, такое расхождение в результатах объясняется не отсутствием учета каких-то статистически не устоявшихся факторов, а присутствием дополнительной силы.

Этой дополнительной силой является электромагнитная сила! Их даже две: 1) сила радиационного излучения самой Земли, 2) магнитная сила.

Вышеприведенные расчеты показывают: чтобы растянуть экваториальный радиус до разницы с полярным в 21 км, центробежной силы явно не хватает.

Как известно, Земля – не холодная планета, и она имеет мощное излучение в инфракрасном диапазоне электромагнитных волн. Особенно сильное излучение в тропической зоне. Это красное (краснофотонное) излучение, я его кратко называю крафонным излучением. На экваторе максимальный нагрев поверхности, здесь максимальное расширение и оттяжка ее в сторону Солнца. По мере удаления на север или на юг (к полюсам) эта сила ослабевает. На полюсах излучение минимально (относительно). Если бы на полюсах была такая же температура, как и на экваторе, то мы наблюдали бы расчетное сжатие. Жаркий пояс Земли занимает около 40% ее поверхности. Посмотрите на рисунок ниже, где отражена тепловая картина нашей планеты.

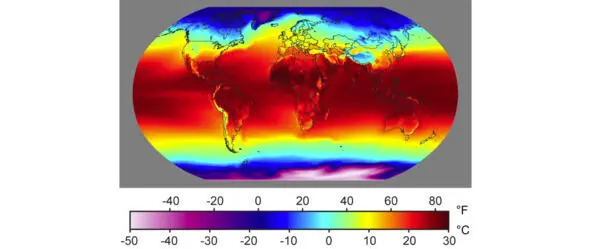
Рис. 2.8. Annual Mean Temperature (Среднегодовая температура) [7]