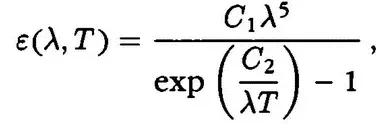Олег Спиридонов - Людвиг Больцман - Жизнь гения физики и трагедия творца

Но способ, которым шел Планк к успеху, был весьма необычным для теоретика. В 1900 г. он докладывает немецкому физическому обществу работу «Об одном улучшении спектрального закона Вина», в которой он «сконструировал совершенно произвольное выражение для энтропии и получил следующую двухконстантную формулу излучения:

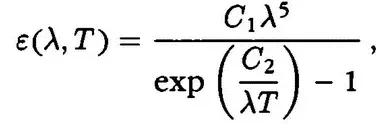
которая, как можно видеть, значительно лучше соответствует опубликованным опытным данным». Этот доклад не вызвал особенного интереса у слушателей, поскольку путь получения новой формулы был совершенно неубедителен. Планк и сам сознавал это.

«Если бы даже формула излучения оказалась совершенно точной, — пишет он, — то она имела бы очень ограниченное значение, исключительно как удачно подобранное интерполяционное выражение. Поэтому я со дня установления этой формулы поставил себе задачей сообщить ей реальное физическое значение. Этот вопрос привел меня к изучению зависимости между энтропией и вероятностью, т. е. к больцмановскому ходу мыслей (выделено мной. — О. С). После нескольких недель наиболее напряженной за всю мою жизнь работы потемки прояснились и передо мной забрезжил свет новых далей».

Еще раз можно отметить направляющую роль Больцмана в прозрении Планка. Об этом же пишет в своей книге «По тропам науки» французский физик Л. де Бройль, вспоминая, что, когда Планк сообщил Больцману о своих первоначальных и неудачных попытках найти формулу излучения, тот ответил ему, что правильную теорию теплового излучения нельзя построить без введения в процессы излучения ранее неизвестного элемента прерывности (дискретности) излучения.

Планк придал реальность этой идее Больцмана, и скоро обнаружилась поразительная плодотворность перенесения атомистических представлений в теорию излучения. Планк ввел так называемую гипотезу естественного излучения, аналогично гипотезе молекулярного хаоса. Ее сутью является то, что отдельные волны, из которых состоит электромагнитное излучение, полностью некогерентны, или, что одно и то же, отдельные излучатели настолько удалены друг от друга, что они непосредственно не взаимодействуют между собой. Мерой энтропии построенной таким образом системы будет, следуя Больцману, число всевозможных «электромагнитно-различных» размещений энергии между излучателями системы. Но для того чтобы вычислить число этих размещений, Планк обязан был предположить, что полная энергия системы складывается из конечного числа элементарных порций энергии, которые он назвал квантами. Нетрудно видеть, что Планк повторяет путь Больцмана, предложенный в работе «Об отношении второго начала механической теории теплоты и исчисления вероятностей в соответствии с теоремами о тепловом равновесии» (1877), однако результат, полученный им, был совершенно иным.

В этой работе Больцман ввел предположение о дискретности энергии молекул лишь как вспомогательный математический прием, как «полезную фикцию». Значение минимальной порции энергии е в окончательные результаты не вошло, так как в ходе расчета Больцман устремлял ее к нулю. Больцман не вкладывал физического смысла в допущение о дискретности энергий молекул, а рассматривал это лишь как способ быстрого решения поставленной перед собой задачи. И все же Планк использует полученный в этой работе результат для определения вероятности состояния системы излучателей, поскольку «в гипотезах, лежащих в основании электромагнитной теории излучения, мы не имеем абстрактно никакого отправного пункта для суждения о такой вероятности». Планк, как и ранее Больцман, рассматривает распределение энергии конечными порциями — квантами — не как свойство самого излучения, а как результат взаимодействия излучения с веществом.

Энергию кванта Планк положил пропорциональной частоте излучения:

где h — введенная им новая постоянная. Полученная в этом предположении формула в точности совпадала с полученным им же ранее выражением. Формула также прекрасно совпадала с экспериментальными данными, и из данных опыта Планк вычисляет значение h:

Постоянная h начала свой путь в физике, ныне же она входит в число универсальных физических постоянных и носит название постоянной Планка.

В ходе теоретических исследований Планк совершенно строго получил формулу Больцмана (14), связывающую энтропию и вероятность, и вычислил значение входящего в нее коэффициента пропорциональности k: