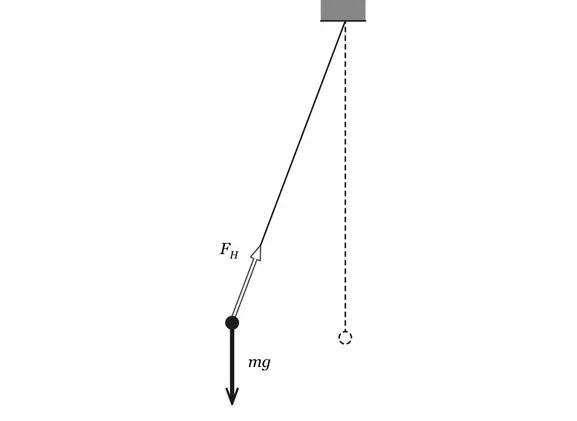
Рис. 1.Математический маятник в поле тяжести Земли. Пунктиром показано положение равновесия, сплошной линией – отклонение от него. Сила натяжения нити F Н и сила тяжести mg , складываясь, порождают возвращающую силу, которая и заставляет маятник колебаться
Вычислитепериод малых колебаний такого математического маятника бесконечной длины. Какой еще известный вам процесс имеет тот же период? Объясните, почему эти два совершенно разных типа движения имеют одинаковый период.
Подсказка 1
Ясно, что бесконечность подставлять в формулу нельзя, поскольку при выводе этой школьной формулы не предусматривалась такая экстремальная ситуация, которую мы предложили в задаче. Значит, надо формулу вывести еще раз – но только с учетом того, что радиус Земли много меньше длины маятника, а не наоборот.
Подсказка 2
Тут есть два подхода: стандартный метод расчета и маленькая хитрость.
Стандартный метод вычисления периода колебаний таков. Рисуем положение равновесия и положение с небольшим горизонтальным отклонением x от него. Выясняем, откуда берется возвращающая сила. Убеждаемся, что возвращающая сила линейно зависит от отклонения, и возникший коэффициент пропорциональности называем жесткостью: F = − kx . Жесткость, деленная на массу грузика, дает частоту ω в квадрате. Период – это 2π/ω .
Маленькая же хитрость заключается в том, что когда вы начнете следовать этой процедуре, то догадаетесь, что задача в некотором смысле эквивалентна исходной. И тогда вы сразу сможете написать ответ без вычислений.
Так или иначе, начните с рисунка исходного положения бесконечно длинного маятника, положения при отклонении от равновесия, нарисуйте силы и найдите возвращающую силу.
Решение
На рис. 2 изображен наш бесконечно длинный маятник. Пунктирной линией показано положение равновесия, сплошной – отклонение от него. Обратите внимание, что смещение вбок – строго горизонтальное, а не по дуге, как на рис. 1, поскольку расстояние до точки подвеса считается неограниченно большим.
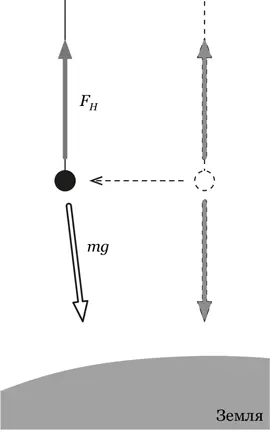
Рис. 2.Бесконечно длинный маятник в поле тяжести Земли
Если бы поле тяжести было строго однородным, то есть всегда направленным вниз, как на рис. 1, то никакой возвращающей силы при строго горизонтальном смещении не возникло бы. Сила вбок возникает на рис. 2 потому, что реальное поле тяжести – неоднородное; сила тяжести направлена в каждой точке не строго вниз, а к центру Земли. При смещении грузика направление на центр отклоняется от вертикали, и именно отклонение от вертикали порождает возвращающую силу.
Обратите внимание, как поменялись ролями две силы! В обычной задаче (рис. 1) сила тяжести всегда направлена вниз, а сила натяжения нити в колеблющемся маятнике отклоняется от вертикали. Здесь все наоборот: направление нити, а значит, и сила ее натяжения все время остаются вертикальными, а отклоняется от вертикали уже сила тяжести. При этом, чтобы сила тяжести не изменялась по абсолютной величине, надо, чтобы угол отклонения был мал, то есть чтобы амплитуда колебания была много меньше радиуса Земли.
Эта неожиданная параллель между двумя ситуациями открывает нам короткий путь к ответу. Возвращающая сила возникает из-за горизонтального дисбаланса двух сил, то есть из-за ненулевого угла отклонения одной силы относительно другой . Этот угол точно такой же, как был бы в исходной школьной задаче с маятником в строго однородном поле тяжести и с длиной, равной радиусу Земли. Мы просто поменяли местами две силы, и задача теперь выглядит стандартной, но только с L = R . А это значит, что мы сразу пишем ответ: 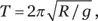 что после подстановки чисел дает примерно 85 минут.
что после подстановки чисел дает примерно 85 минут.
Это выражение точь-в-точь совпадает с периодом движения спутников по круговой орбите вокруг Земли. И это, конечно, не случайность, как мы сейчас увидим.
Послесловие
В принципе, интуитивно понятно, что эти два вида движения – малые колебания туда-сюда бесконечно длинного маятника над поверхностью Земли и свободное движение спутника вокруг Земли – должны быть как-то связаны. В обоих случаях все определяется притяжением к Земле, да и размер в нашем распоряжении только один – ее радиус. Но все же для пущей убедительности хочется увидеть , как именно эти два движения связаны друг с другом, почему у них одинаковый период.
Читать дальше



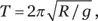 что после подстановки чисел дает примерно 85 минут.
что после подстановки чисел дает примерно 85 минут.










