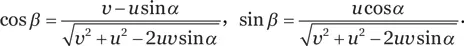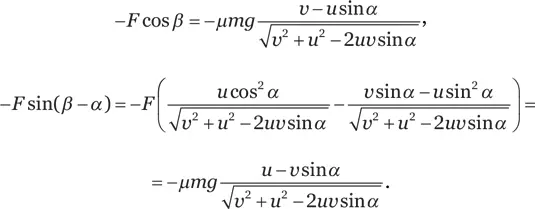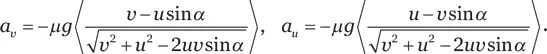Игорь Иванов - Как ломаются спагетти и другие задачи по физике

Рассмотрим участок кольца, который находится под углом α к направлению движения (рис. 2). Пусть в данный момент времени скорость центра масс кольца равна v , а скорость вращения обода u = ωR , где ω – угловая скорость вращения в данный момент, а R – радиус кольца. Этот кусочек кольца участвует в поступательном и вращательном движении. Его скорость относительно поверхности показана на рисунке серой стрелкой. Она составляет угол β с направлением поступательного движения, причем

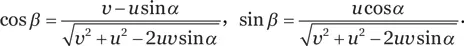
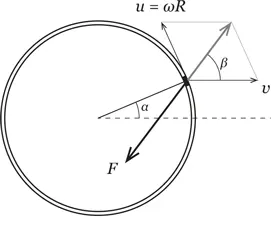
Рис. 2.Скорости и силы на маленьком участке кольца

Эти выражения выглядят громоздкими, но они получаются из обычных формул сложения двух векторов скоростей.

Сила трения, действующая на этот участок, по модулю равна F = μmg (здесь m – масса участка кольца) и направлена в противоположную от скорости сторону. У этой силы есть проекция на направление поступательного движения, – F cos β , и проекция на касательную к кольцу, которая притормаживает вращение, – F sin ( β – α ). Не стесняясь, подставим сюда выражения для синуса и косинуса угла β , а также учтем, что sin ( β – α ) = sin β cos α – cos β sin α :

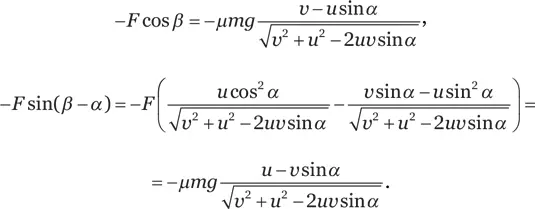
У этой силы есть также проекция вбок, то есть перпендикулярно поступательному движению, но при усреднении по всему кольцу эта проекция обнулится. В этом можно убедиться математически, если рассмотреть второй участок, находящийся под углом π – α . Для него построение аналогичное, две притормаживающие проекции будут такими же, а сила вбок – ровно противоположная.

Для того чтобы посчитать эффект для всего кольца в целом, надо сложить эти силы по всему кольцу, то есть учесть элементы кольца, расположенные под всеми углами α . Это даст нам два ускорения, притормаживающих поступательное движение и вращение:

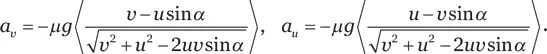
Угловые скобки обозначают усреднение по всем углам α ; это последствие того, что мы общую силу поделили на общую массу. При желании его можно выразить через интегралы, но это не обязательно.

Заметьте интересную особенность полученных формул: при замене u на v выражения для a u и a v превращаются друг в друга. Такая «дуальность» задачи автоматически означает, что если бы начальные скорости u и v были равны, то ускорения a u и a v тоже были бы одинаковые и, значит, соотношение u = v выполнялось бы всегда, до самой остановки. А это, в свою очередь, означает, что вращение и скольжение в данном случае прекратятся одновременно . Смотрите, произошло математическое «чудо»: мы, просто глядя на формулы, вдруг получили ответ для нашей задачи, по крайней мере для одного начального состояния!

А что изменится, если начальные скорости u и v различаются? Тогда ускорения тоже будут отличаться, и, казалось бы, заранее не понятно, что будет замедляться быстрее. Чтобы выяснить, может ли при этом вращение остановиться раньше скольжения, рассмотрим ситуацию, когда скорость вращения u много меньше скорости поступательного движения v . Тогда для поступательного ускорения мы получим примерно a v= −μg , словно вращения и не было. Для вращательного ускорения a u получим маленькую величину порядка −μg·u/v, поскольку «большой» вклад, пропорциональный синусу, обнулился после усреднения по всем углам (более точное выражение см. в послесловии). Иными словами, если вращение очень медленное, то оно и замедляется намного медленнее, чем скольжение. Можно сказать и так: относительное замедление вращения ( a u/u ) пропорционально относительному замедлению скольжения ( a v/v ). Отсюда и следует, что скольжение и вращение не могут прекратиться в разные моменты времени.

Выше мы отметили, что задача математически симметрична относительно замены поступательного движения на вращательное. Поэтому мы совершенно аналогичным способом получаем и второй вывод: если поступательное движение намного медленнее вращения, то и замедляться оно будет намного медленнее вращения. Соответственно, и в этом случае нет никакой возможности остановить скольжение раньше вращения.