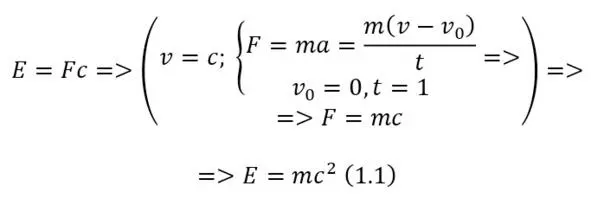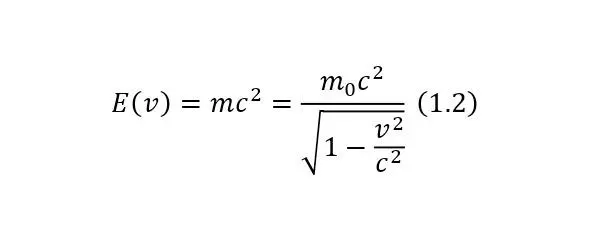Ибратжон Алиев - Все науки. №1, 2022. Международный научный журнал

Таким образом было открыто новое множество, в которое входят все вышеперечисленные множества, то есть натурное, рациональное, иррациональное и действительные множества, такое множество и было названо комплексным.

Следовательно, чтобы прийти к явным математическим парадоксам и удивительным явлениям, необходимо исходить из физического явления, который ранее ещё некогда был опубликован в 1905 году в статье Альберта Эйнштейна «К электродинамике движущихся тел», которая также была основана на преобразовании Х. Лоренца, работ Дж. Лармора, Анри Пуанкаре и других. Изначально, достаточно воспользоваться знаменитым выводом (1.1), который выходит к (1.2).

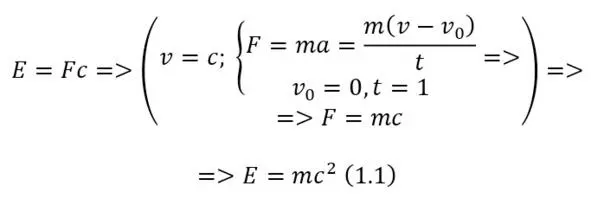
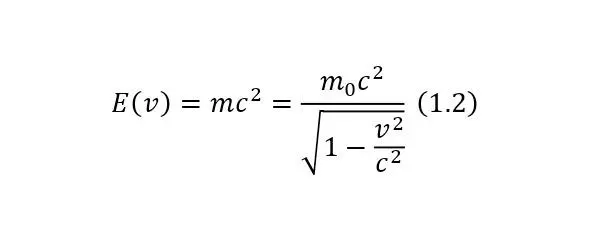
Это равенство несёт глубокий физический смысл, но если рассматривать его как функцию, то можно рассмотреть 3 случая:

1. Если скорость тела меньше скорости света;

2. Если скорость тела равна скорости света;

3. Если скорости тела больше скорости света.

Таким образом из этих 3 случаев получаются 4 вида чисел. Первый из них – действительные числа, а второй – комплексные числа. Далее следуют два неизвестных ранее видов чисел, а именно числа, которые могут делиться на ноль, а также числа, которые больше этого вида чисел.

И конечно, прогресс не стоит на месте и сегодня уже исследованы и открыты различные физические явления, всё ещё ожидающие своего объяснения и математической трактовки. Ярким примером является явление запутанных частиц, то есть это явление, в котором образуются два запутанных лептона, а именно два электрона или фотона, информация о спине которых передаётся после определения или изменения спина одного к другому со скоростью, намного превышающей скорость света – 3 случай.

Также сам факт наличия световых волн, также известных в виде корпускул как фотоны, заставляет задуматься о моменте, когда скорость объекта стала бы равной скорости света – 2 случай.

И чтобы описать все эти явления, возникла необходимость создания нового раздела математики, известного как «Ингенциальная математика», от латинского ingens – «огромные». В этом случае принимается наличие ингенциальной единицы, то есть дроби единицы на ноль, после чего образуются различные арифметические, алгебраические и иные виды операций, преобразуя как тригонометрические, логарифмические, обратно-тригонометрические и иные функции, так и вводя совершенно новые виды операций.

Но перед тем, как перейти к третьему случаю, стоит уточнить, что благодаря выводу основной энергетической функции, определяется местоположение ингенциальных чисел на числовой оси, а именно эти числа являются большими бесконечности, а значит является вершиной всех множеств, охватывая каждое из них, в том числе и комплексное множество. Также при этом определяется, что комплексные числа являются наименьшими и находятся уже между промежутками натуральных чисел. Также можно определить третий вид чисел как дроби единицы и комплексного числа. При этом эти виды чисел называются пер-ингенциальные от латинского per-ingens – «сверхогромный». Этот вид чисел является ещё более большим чем ингенциальные числа и обладает ещё более завораживающими свойствами, которые ещё только предстоит подробнее исследовать, впрочем, как и все остальные.

1. Балк М. Б., Балк Г. Д., Полухин А. А. Реальные применения мнимых чисел. – Киев: Радянська школа, 1988. – 255 с.

2. Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. – изд. 13-е. – М.: Наука, 1985. – 544 с.

3. Бугров Я. С., Никольский С. М. Высшая математика. Том первый: элементы линейной алгебры и аналитической геометрии. М.: Дрофа, 2004. – 288 с.

Аннотация.Недавно исследованные ингенциальные числа обладают довольно экзотическими и заманчивыми свойствами среди разновидности остальных чисел, порождая особые свойства в множестве алгебры, что отражается также и при описании с их помощью многочисленных физических явлений, большинство из которых можно отнести к явлениям релятивистской физики.