Стивен Вайнберг - Пояснюючи світ

У Ґраці Кеплер почав листуватися з Тіхо Браге, який перед тим прочитав «Таємницю світу». Тіхо запросив Кеплера відвідати його в Ураніборзі, але Кеплер подумав, що це була б надто далека подорож. Тоді в лютому 1600 року Кеплер прийняв запрошення Тіхо відвідати його у Празі, що з 1583 року була столицею Священної Римської імперії. Там Кеплер почав вивчати дані, які отримав Тіхо, особливо про рухи Марса, і знайшов розбіжність у 0,13° між цими даними та теорією Птолемея [40].

Кеплер і Браге не дуже добре ладнали між собою, і Кеплер повернувся до Ґраца. Саме в цей час протестантів із Ґраца виганяли, і в серпні 1600 року Кеплеру з родиною довелося звідти поїхати. Повернувшись до Праги, Кеплер почав разом із Браге працювати над «Рудольфовими таблицями» – новими астрономічними таблицями, що мали замінити «Прусські таблиці» Рейнгольда. Після смерті Тіхо Браге в 1601 році кар’єрні проблеми Кеплера на деякий час були розв’язані його призначенням на місце Тіхо придворним математиком імператора Рудольфа II.

Імператор прихильно ставився до астрології, тому обов’язки Кеплера на посаді придворного математика передбачали також укладання гороскопів. Цією справою він успішно займався ще за часів студентства в Тюбінґу, попри його власний скептицизм щодо астрологічних передбачень. На щастя, у нього також залишався час для справжньої науки. У 1604 році він виявив за допомогою спостережень нову зірку в сузір’ї Змієносця – наднову (чого в нашій галактиці або поблизу неї не помічали більше аж до 1987 року). Того самого року він опублікував Astronomiae Pars Optica («Оптична частина астрономії») – працю з оптичної теорії та її застосування до астрономії, включно із впливом заломлення світла в атмосфері на спостереження планет.

Кеплер далі вивчав рух планет і безуспішно намагався узгодити точні дані Тіхо Браге з теорією Коперника, додаючи ексцентри, епіцикли та екванти. Цю працю він закінчив до 1605 року, але її опублікування відклали через суперечку зі спадкоємцями Тіхо. Нарешті в 1609 році Кеплер опублікував свої результати у творі Astronomia Nova («Нова астрономія, ґрунтована на причинних зв’язках, або Небесна фізика, викладена в коментарі про рухи Марса»).

Частина III цього твору істотно уточнила теорію Коперника, ввівши еквант та ексцентр для Землі так, що з’являється точка, розташована з протилежного боку від центру Землі відносно її орбіти. Відносно цієї точки Земля обертається з постійною кутовою швидкістю. Це усунуло більшість невідповідностей, що заплутували планетні теорії з часів Птолемея, але дані Тіхо Браге були достатньо добрі, щоб Кеплер міг бачити, що певні конфлікти між теорією й спостереженнями все ж залишаються.

У якийсь момент Кеплер переконався: це завдання не розв’язати і йому доведеться відкинути припущення, спільні для Платона, Арістотеля, Птолемея, Коперника та Браге, що планети рухаються круговими орбітами. Натомість він зробив висновок, що планетні орбіти мають еліптичну форму. Врешті в розділі 58 (із 70) «Нової астрономії» Кеплер сказав про це чітко. У положенні, що пізніше стало відомо як перший закон Кеплера, науковець зробив висновок, що планети (включно з Землею) обертаються по еліпсах, із Сонцем у фокусі, а не в центрі.

Так само, як коло повністю описується (крім місця його розташування) єдиним числом – його радіусом, будь-який еліпс можна повністю описати (крім місця його розташування та орієнтації) двома числами, які є довжинами його довшої та коротшої осей, або числами, одне з яких є довжиною довшої осі, а друге – числом, відомим як ексцентриситет, що говорить нам, наскільки різними є більша та менша осі (див. технічну примітку 18). Два фокуси еліпса є точками на довшій осі, рівновіддаленими від центра, відстань між якими дорівнює добутку ексцентриситету на довжину довшої осі еліпса. За нульового ексцентриситету дві осі еліпса мають рівну довжину, два фокуси зливаються в єдину центральну точку – і еліпс перетворюється на коло.

Насправді орбіти всіх відомих Кеплеру планет мають невеликі ексцентриситети, як це показано нижче в таблиці сучасних значень (спроектованих на 1900 рік):

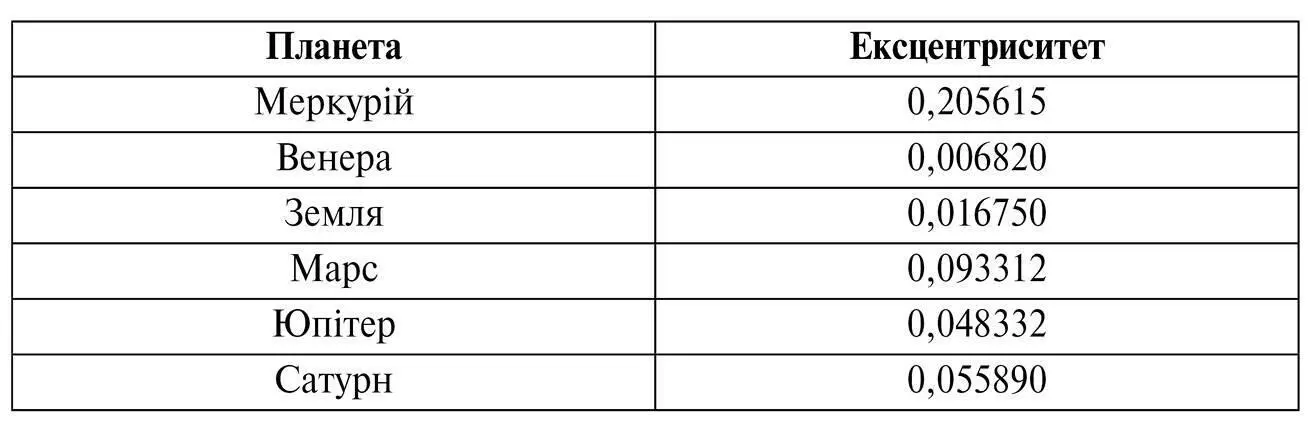
Ось чому спрощені версії теорій Коперника та Птолемея (без жодних епіциклів у теорії Коперника й лише з одним епіциклом для кожної із п’яти планет у теорії Птолемея) мали б працювати доволі добре [41].