Лоуренс Краусс - Почему мы существуем? Величайшая из когда-либо рассказанных историй

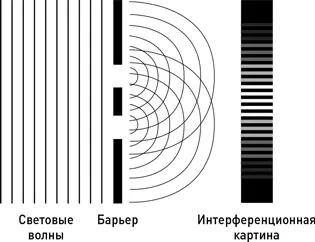
Использовав именно такой аппарат с узкими щелями, Юнг увидел на стене картину интерференции, характерную для волн, и таким образом наглядно продемонстрировал волновую природу света. Это событие, имевшее место в 1804 г., стало важной вехой в истории физики.

Можно проделать тот же эксперимент, что и Юнг, но не со светом, а с элементарными частицами, к примеру с электронами. Если направить пучок электронов на фосфоресцентный экран (скажем, экран старого электроннолучевого телевизора), мы увидим яркую точку в том месте, где пучок электронов попадает на экран. Теперь давайте поставим перед экраном две щели, как делал Юнг в эксперименте со светом, и направим на экран широкий пучок электронов.

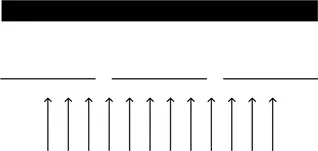
Основываясь на тех же рассуждениях, которые я приводил для света, можно было бы ожидать появления двух ярких линий за каждой из щелей, через которые электроны проходят к экрану. Однако как вы, вероятно, уже догадались, на самом деле получится нечто иное, по крайней мере если щели достаточно узки и близки друг к другу. Вы увидите интерференционную картину, аналогичную тем, что наблюдал Юнг для световых волн. Получается, что электроны, представляющие собой частицы, в данном случае ведут себя в точности как световые волны. В квантовой механике частицы обладают волновыми свойствами.

Тот факт, что электронные «волны», исходящие из одной щели, могут интерферировать с электронными «волнами», исходящими из другой, конечно, является неожиданным и странным, но гораздо более странно то, что происходит, если мы посылаем электроны к экрану по одному . Даже в этом случае на экране возникает такая же интерференционная картина. Каким-то непонятным образом каждый электрон интерферирует сам с собой. Электроны определенно не похожи на бильярдные шары.

Интерпретировать это можно следующим образом. Вероятность попадания электрона в каждую точку экрана можно определить, если считать каждый электрон летящим не по одной-единственной траектории, а по множеству различных траекторий одновременно , причем некоторые из этих траекторий проходят через одну щель, а некоторые – через другую. Затем те, что проходят через первую щель, интерферируют с теми, что проходят через вторую, – и формируют наблюдаемую на экране интерференционную картину.

Проще говоря, нельзя утверждать, что электрон проходит либо через одну, либо через другую щель, как бильярдный шар. Получается, что электрон проходит не через одну из щелей, а через обе щели одновременно.

Вздор, скажете вы и предложите вариант эксперимента, при помощи которого можно было бы это доказать. Установим регистраторы электронов возле каждой из щелей: они должны щелкать, когда через соответствующую щель пролетит электрон.

И действительно, когда электроны по одному летят к экрану, каждый раз срабатывает лишь одно устройство. Так что каждый электрон, судя по всему, все же проходит только через одну щель, а не через обе одновременно.

Однако если вы теперь посмотрите на рисунок, образованный электронами на экране позади щелей, то окажется, что он изменился и теперь вместо первоначальной интерференционной картины там наблюдается то, что мы ожидали увидеть с самого начала: яркая область за каждой из двух щелей, как если бы экран обстреливали не волнами, а миллиардами шариков или пуль.

Иными словами, пытаясь проверить нашу классическую интуицию, мы изменили поведение электронов. Или, как чаще говорят в квантовой механике, измерение состояния системы может изменить ее поведение.

Один из многих невозможных на первый взгляд аспектов квантовой механики заключается в том, что не существует такого эксперимента, который позволяет продемонстрировать, что в отсутствие измерений электроны ведут себя добропорядочным, классическим образом.

Странная волноподобная природа объектов, таких как электроны, которые вместе с тем могут рассматриваться и как частицы, математически выражается приписыванием каждому электрону так называемой волновой функции , которая описывает вероятность нахождения этого электрона в любой заданной точке. Если волновая функция принимает ненулевые значения во множестве различных точек, то это означает, что положение электрона не может быть определено заранее, до точного измерения его местонахождения. Иначе говоря, есть ненулевая вероятность, что электрон вовсе не находится в некоторой конкретной точке пространства до того, как он обнаружен там измерением.