Джирл Уокер - Новый физический фейерверк

ОТВЕТ •Когда вы вытягиваете пружину сначала вверх, а потом опускаете на следующую ступеньку, вы пускаете по длине пружинки волну. Когда волна начинает распространяться по пружинке, витки сначала поднимаются вверх, а потом по дуге пружинки спускаются вниз — на нижнюю ступеньку, и постепенно туда переходит все больше витков. Когда волна дойдет до последних витков, оставшихся на верхней ступеньке, их с достаточно большой скоростью протащит по дуге, они перелетят над второй ступенькой и (если размеры ступеньки подобраны правильно) остановятся на третьей. После этого процесс повторится.

Кувыркаться вниз по ступенькам (причем достаточно медленно, так что вы видите этот неторопливый спуск) слинки может за счет прямоугольного сечения провода, из которого сделана пружинка. Для этой конструкции, запатентованной в 1947 году Ричардом Джеймсом, характерно меньшее отношение жесткости пружины к ее массе по сравнению с такой же пружинкой, сделанной из провода с круглым сечением. Меньшее значение этого отношения приводит к тому, что волна, которую вы пускаете вдоль длины пружины, распространяется с меньшей скоростью. Пластмассовые слинки, у которых другое значение этого отношения и, соответственно, другая скорость распространения волны, кувыркаются с вдвое меньшей скоростью, чем первые слинки, сделанные из металла.

Но в любом случае время для спуска слинки на одну ступеньку определяется отношением жесткости пружинки к ее массе, а не высотой ступеньки. На невысоких ступеньках волна распространяется медленно, на высоких — быстрее, но время, требуемое для пробегания волны по всей длине растянутой пружинки, одинаково для обеих ступенек.

Поставим друг на друга на край стола книги, костяшки домино, карты, монетки или другие одинаковые плоские предметы так, чтобы стопка свисала с края стола. Как нужно расположить эти предметы, чтобы при заданном их количестве длина навеса (расстояния по горизонтали от края стола до края самой выступающей части стопки) была максимальной? Предположим, что вы укладываете костяшки домино длиной L . Сколько нужно костяшек, чтобы навес был равен L ? А 3 L ?

У вас есть комплект из 28 костяшек домино. Постройте арку между двумя столами одинаковой высоты. Что нужно сделать, чтобы арка была максимально длинной?

Кубики «лего» — это игрушечные пластмассовые параллелепипеды. На одной из широких сторон детали сделано четыре углубления, а на противоположной стороне находятся четыре небольших штырька. Одну деталь можно соединить с другой так, чтобы четыре штырька первой вошли в соответствующие отверстия второй, а можно и так, чтобы верхняя деталь была сдвинута на половину длины, то есть только два ее штырька вошли в два отверстия нижнего. Пусть x — половина длины грани детали, а n — количество деталей. Сколько различных типов устойчивых (не падающих без поддержки) башен можно собрать из этого количества деталей?

Рассмотрим башню, в которой каждая деталь, за исключением самой нижней, установлена либо прямо над предыдущей, либо сдвинута вправо относительно предыдущей. Какое минимальное количество деталей нужно взять, чтобы навес всей стопки был равен, скажем, 4 x ? Есть ли более рациональный способ укладывания в стопку при том же самом навесе?

ОТВЕТ •Стопка находится в равновесии, если вертикальная линия, проведенная через ее центр масс, не выходит за границы стола. Таким образом, чтобы добиться наибольшего навеса, нужно, чтобы эта вертикаль проходила через самый край стола. Один из способов получить большой навес основан на гармонических рядах (рис. 1.22а). Допустим, мы строим башню из костяшек домино. Чтобы уравновесить костяшку, нужно положить ее так, чтобы ее центр приходился на край стола, и тогда получим навес, равный L /2. Потом положим на нее следующую костяшку и сделаем так, чтобы общий центр масс двух костяшек приходился на край стола. Навес теперь будет равен ( L /2)(1 + 1/2). Потом положим на них третью костяшку и уложим стопку так, чтобы центр масс трех костяшек приходился на край стола. Новый навес будет равен ( L /2)(1 + 1/2 + 1/3). Когда башня будут построена из n костяшек домино, навес башни будет равен ( L /2)(1 + 1/2 + 1/3 + … +1/ n ), где выражение в скобках — гармонический ряд. Приведу несколько результатов.

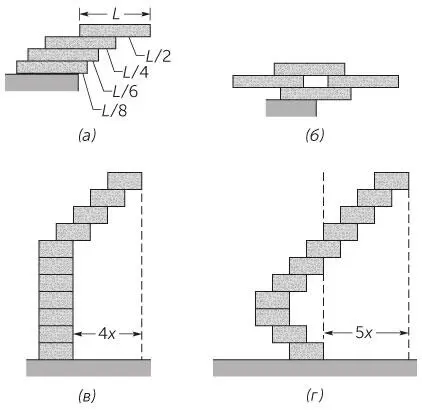
Рис. 1.22 / Задача 1.66.Башни из костяшек домино (а) — (б) и деталей «лего» (в) — (г).