Грегори Гбур - Загадка падающей кошки и фундаментальная физика

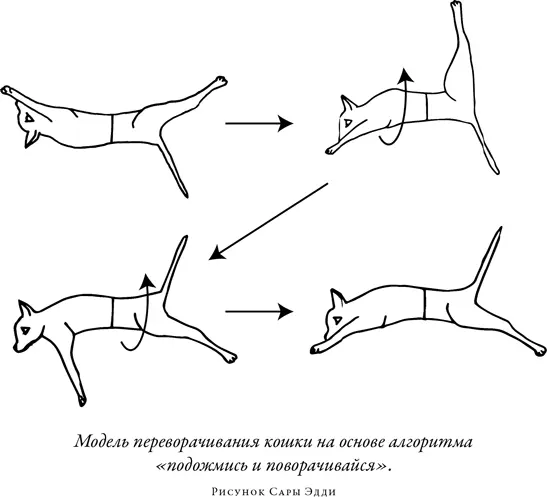
Марей поддержал это объяснение, и позже оно получило известность как модель переворачивания кошки типа «подожмись и поворачивайся». Качественное объяснение Гийю поддержал и Морис Леви, который при помощи строго математического анализа, основанного на теореме площадей, показал, что это объяснение по крайней мере правдоподобно с физической точки зрения. Даже Марсель Депре, один из самых яростных защитников Делоне, в конечном итоге принял новый взгляд на теорему площадей и, замечательно извернувшись, припомнил, что именно он побудил Марея сделать те самые фотографии падающей кошки.

Мне казалось, что способности, которыми пользуется животное для получения этого замечательного результата, с точки зрения приведенной выше теоремы [теоремы Делоне] обладают огромной важностью, но, не имея в своем распоряжении никакого устройства для мгновенной фотографии, я подумал, что лучше всего будет рассказать о своих идеях мистеру Марею, который имеет все средства исследования, которых у меня нет, и я несколько раз при случае выразил ему пожелание обратиться к этому вопросу возможностями мгновенной фотографии. Сегодня я доволен своей настойчивостью, потому что опыт, результаты которого он представил Академии, привлек, как я ему сказал, внимание к следствиям из теоремы площадей и высветил ту ошибку, жертвами которой стал не только Делоне, но и все авторы трактатов по теоретической механике {11} .

Объяснения и Гийю, и Леви появились сразу же после публикации в журнале Comptes Rendus статьи Марея, посвященной его фотографиям; похоже, академики спешили оправдаться после тех насмешек со стороны СМИ, которым они подверглись. Даже научные публикации на эту тему часто не обходились без забавных деталей; так, в описание фотографий Марея в журнале Nature входила оценка позиции самой кошки: «Выражение оскорбленного достоинства, продемонстрированное кошкой в конце первой серии фотографий, указывает на недостаток интереса к научному исследованию с ее стороны» {12} .

Из академической дискуссии, однако, было неясно, действительно ли алгоритм Гийю описывает способ, при помощи которого кошки переворачиваются на самом деле . Тем не менее это объяснение было принято как факт и через несколько лет попало даже в учебники по физике. Этот пример, в частности, содержится в книге по «динамике системы твердых тел» 1897 г. издания:

Пример 3. Объясните, как кошка, которую подняли лапами кверху и отпустили, оказывается, упав с достаточной высоты, в правильном положении и приземляется на лапы.

На первом этапе падения кошка вытягивает задние лапы почти перпендикулярно оси тела и подтягивает передние к шее. В этом положении она поворачивает переднюю часть тела на как можно больший угол; при этом задняя часть тела поворачивается на меньший угол в обратном направлении, так что полная сохраняющаяся площадь относительно этой оси равна нулю… На втором этапе падения положение лап меняется на обратное, задние поджимаются к телу, а передние вытягиваются. Теперь кошка поворачивает заднюю часть тела на больший угол, а переднюю в обратном направлении — на меньший. В результате обе части тела кошки оказываются повернутыми вокруг оси на почти одинаковые углы {13} .

Хотя задача, кажется, была наконец решена, не следует переоценивать влияние, произведенное откровением падающей кошки на мышление физиков того времени. Марей при помощи всего лишь небольшого числа фотографий наглядно продемонстрировал две важные истины. Первая состоит в том, что, хотя законы физики, такие как закон сохранения момента импульса, невозможно нарушить, их можно «обойти» самыми неожиданными способами, которые делают возможными вещи, на первый взгляд кажущиеся невозможными. Вторая истина — то, что природа давно уже нашла многие пути «обхода» и что более тщательное исследование природы потенциально может оказаться полезным в решении задач, которые ставят ученых в тупик.

Статьи, посвященные задаче падающей кошки, продолжали выходить в Comptes Rendus на протяжении еще нескольких месяцев после публикации работы Марея; в них авторы продолжали разрабатывать поднятую тему. В одной из таких статей, написанной Леоном Лекорню в конце 1894 г., отмечается, что другие животные, в принципе, могут использовать для переворачивания другие стратегии:

Еще более простой пример переворачивания за счет внутренних сил можно увидеть в движении змеи, если представить себе, что она изогнута на плоскости в форме тора и ее сечения вращаются, каждое в своей плоскости, с одинаковой угловой скоростью. Теорема площадей при этом, очевидно, будет соблюдаться, а внешняя форма змеи не только будет оставаться постоянной, но и покажется неподвижной в пространстве, несмотря на то что спинка змеи при этом окажется на месте ее живота и наоборот. Нет ничего невозможного в том, чтобы подобный процесс использовался некоторыми водными животными {14} .