Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

Однако оказалось, что два фермиона при определенных условиях можно объединить в единую «частицу», которая уже не станет следовать принципу Паули. Для этого необходимо иметь какое-то притяжение между ними – «клей», который соединит их в составной бозон. Именно благодаря такому спариванию электронов в металле и возникает явление сверхпроводимости.

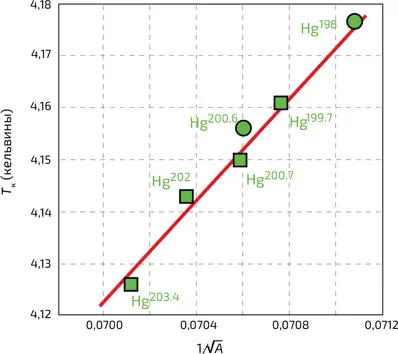
7. Критическая температура различных изотопов ртути. Массовое число A соответствует общему количеству нуклонов (протонов и нейтронов). Напомним, что два изотопа имеют одинаковое количество протонов (у ртути их 80), но разное число нейтронов и, следовательно, обладают разной массой. Молярная масса каждого изотопа указана рядом с обозначением, в г/моль. (По Reynolds et al., Phys. Rev. 78, 487 (1950))

Какого же рода притяжение вызывает такое объединение электронов? Его существование совсем не очевидно: в самом деле, как известно, две частицы одного и того же заряда должны отталкиваться друг от друга! Однако, как обнаружил в 1950 году английский физик Герберт Фрёлих, если эти электроны находятся не в вакууме, а в кристалле, то такое притяжение может иметь место. Действительно, в кристалле ионы упорядочены в кристаллическую решетку, которая может деформироваться. Сила притяжения между двумя электронами в присутствии этой решетки связана с ее упругостью. Присутствие в ней электрона вызывает локальную деформацию, которая способствует притяжению второго электрона.

В качестве нестрогой аналогии можно привести пример двух шариков, лежащих на резиновом коврике. Если эти шарики далеки друг от друга, то каждый из них деформирует коврик, образуя вокруг себя лунку. Если же положить сначала один шарик, а затем невдалеке от него другой, то их лунки сольются в одну и шарики скатятся вместе на дно общей лунки. В металлах подобное притяжение возникает вследствие деформации кристаллической решетки.

На выявление столь важной для объяснения явления сверхпроводимости роли упругих колебаний решетки [30] Выражение «упругие колебания» часто заменяется термином «фононы». Фононы – кванты этих колебаний, подобно тому как фотоны – кванты света. Оба слова происходят от греческих φως («свет») и φωνη («звук»); и в самом деле, упругие колебания кристаллической решетки отвечают за распространение звука. (или фононов) в значительной степени повлияло открытие в 1950 году изотопического эффекта (илл. 7). Оказалось, что два изотопа одного и того же металла имеют различные критические температуры, величины которых обратно пропорциональны квадратному корню из массы изотопа! Это свойство напоминает тот факт, что частота колебаний закрепленного на конце пружины шара зависит от его массы (см. главу 12, врезку «Колебания пружины и пузырька»).

Обнаружение влияния свойств кристаллической решетки вещества на его сверхпроводящие свойства сыграло решающую роль для понимания происхождения этого явления и создания его микроскопической теории. Уже Фрёлих был на верном пути, однако найденное им электрон-фононное притяжение оказалось довольно слабым по сравнению с электростатическим отталкиванием между электронами, и он не сумел объяснить, как оно может обеспечить формирование составных бозонов.

Спустя семь лет после публикации теории Гинзбурга – Ландау американские физики Джон Бардин, Леон Купер и Роберт Шриффер построили теорию сверхпроводимости (так называемую теорию БКШ), которая дала последовательное микроскопическое объяснение этого загадочного явления и сняла все существующие к тому времени противоречия.

В металле при нулевой температуре электроны занимают все энергетические состояния вплоть до некоторой величины Ɛ Ф , называемой энергией Ферми (последняя зависит от концентрации электронов в металле и симметрии его решетки). При этом каждое состояние в соответствии с принципом запрета Паули занято только одним электроном. Энергия Ферми в металлах обычно составляет величину порядка нескольких электронвольт.

Что же касается электрон-фононного взаимодействия, то соответствующие ему энергии определяются так называемой дебаевской частотой W D и не превышают 0,1 эВ. О кулоновском отталкивании электронов можно было бы предположить, что его характерная величина составляет e 2/ a , где величина a соответствует межатомному расстоянию. Легко оценить, что эта величина также оказывается порядка электронвольта. Как же тогда устроить притяжение между электронами?