Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

При варке спагетти они, как правило, сплетаются между собой. Тем не менее авторы этой книги никогда не замечали, чтобы спагетто сам по себе завязался в кастрюле в узел. Дело в том, что спагетто слишком короток!

Для каждого длинного и гибкого объекта (спагетто, шнурок, веревка, кабель и т. д.) существует критическая длина L c , при превышении которой формирование узла практически неизбежно, в то время как при меньшей длине вероятность завязывания невелика. Физики заинтересовались этим явлением не потому, что они очень любят макароны. Причиной их любопытства являются другие длинные и гибкие объекты – полимеры (см. врезку «Полимеры»).

Итак, исследователи полимеров рассчитали критическую длину L c : она пропорциональна другой длине ξ, характеризующей гибкость объекта. Эта последняя соответствует длине, необходимой для того, чтобы цепь полимера могла изменить свое направление на прямой угол (около 3 см для сваренного спагетто). Итак, получим:

L c = γξ.

Задача состоит в том, чтобы вычислить коэффициент пропорциональности γ на основании вероятности образования узла. Чтобы его оценить, физики рассмотрели все конфигурации веревки заданной длины и высчитали, какая их часть образует по крайней мере один узел. Они пришли к выводу, что коэффициент γ составляет порядка 300 – значительная величина! Таким образом, чтобы запутаться в узел с практически стопроцентной вероятностью, спагетто должен иметь длину 10 м!

Однако мы довольно часто видим запутывающиеся шнурки и провода наушников (илл. 5). Английский писатель Джером К. Джером в своем романе «Трое в лодке, не считая собаки» выразил сожаление по поводу склонности веревок к образованию безнадежно запутанных узлов (см. врезку). Соответствует ли это наблюдение выведенной нами выше формуле и примерному значению γ = 300? В этом можно усомниться, так как изученная упрощенная модель не обязательно применима к описанной Джеромом веревке.

5. Поскольку веревка длинная и гибкая, она, скорее всего, запутается… К величайшему раздражению моряков!

Никому и в голову не придет идея попробовать связать узлом сухой спагетто, однако попытка сделать это приведет к неожиданному наблюдению. Возьмем сухой спагетто за два конца (по одному в каждой руке) и начнем постепенно его сгибать. Очевидно, в конце концов он сломается. Интуитивно мы ожидаем, что он разломится на две части. Но на самом деле в результате разлома он распадется на три кусочка или даже больше! Это удивительное явление привлекало внимание многих физиков, в частности Ричарда Фейнмана (1918–1988). Однако лишь в 2005 году два французских физика, Одоли и Нойкирш, сумели пролить свет на физику разлома спагетти.

Для этого они изучили поведение упругого стержня, равномерно сгибаемого при закрепленных концах. Когда его кривизна достигает некоторой критической величины, происходит первый разлом: как и следовало ожидать, в самой хрупкой точке стержня (например, там, где имеется возникшая при сушке спагетто трещинка). Можно было бы подумать, что два фрагмента стержня, удерживаемые за их концы, после нескольких колебаний просто застынут, придя в свои положения равновесия. На самом же деле следует учитывать еще одно, связанное с первоначальным изломом, явление, а именно, резкий излом приводит к возбуждению изгибных волн, которые начинают распространяться по обоим фрагментам спагетто. Прохождение такой волны есть не что иное, как периодическая деформация, накладывающаяся на ту, которая уже существовала в спагетто до разлома. Таким образом, суммарная деформация в некоторых точках фрагмента может превысить критическую величину и, следовательно, вызвать новые переломы. Одоли и Нойкирш убедились в правильности своих теоретических расчетов, засняв процесс разлома спагетто на высокоскоростную камеру (илл. 6).

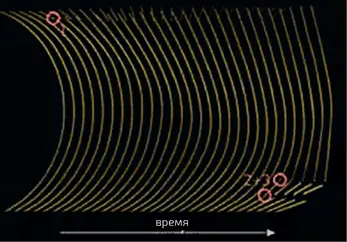
6. Разлом закрепленного на концах спагетто, который сначала изогнули, а затем отпустили. Последовательные кадры были сняты с интервалом в 1/1700 секунды. Первый разлом происходит в точке (1). Затем возбужденная изгибная волна распространяется вдоль спагетто , вызывая локальное изменение кривизны. Два других одновременных разлома происходят в точках (2) и (3). (По B. Audoly, Institut d’Alembert, CNRS et Université Paris 6)