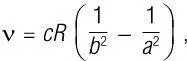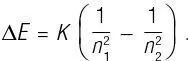Скотт Бембенек - Механизм Вселенной - как законы науки управляют миром и как мы об этом узнали

«Перспективный объект спектроскопии — изучить колебания атомов и молекул, чтобы получить всю возможную информацию о природе сил, связывающих их воедино… Но нам не следует так скоро ожидать открытие какого-то грандиозного и очень общего закона: состав того, что мы называем молекулой, очень сложен, а трудность проблемы настолько велика, что если бы не первостепенная важность результатов, которые, как мы можем надеяться, будут окончательно получены, то всему в этой проблеме, за исключением ее наиболее оптимистичных сторон, возможно, было бы отказано во включении в исследование, которое даже после многих лет работы может оказаться безуспешным».

Бор подготовил для Резерфорда проект со своими исходными идеями, касающимися атомов (в нашем предыдущем обсуждении кратко изложены его наиболее значительные части), в июле 1912 года, но ни слова не сказал об атомных спектрах. На то, чтобы Бор стал серьезно рассматривать атомные спектры в рамках своей теории, уйдет еще год. Его интерес вызвала занимательная беседа с Гансом Мариусом Хансеном (1886–1956).

Хансен занимался спектроскопией в Геттингене. Он поинтересовался, не пытался ли Бор использовать для предсказания спектров его теорию. Бор заметил, что он не уделял ей особого внимания, поскольку успех этой теории казался маловероятным. Хансен настаивал, что Бору следует пересмотреть свою точку зрения, и указал ему на интригующую спектральную формулу, известную как формула Бальмера .

В 1849 году Иоганн Бальмер (1825–1898) защитил докторскую диссертацию в Базельском университете, Швейцария. Он прожил в Базеле всю свою жизнь, работая учителем в женской школе и читая лекции в университете. Бальмер, любитель нумерологии, считал, что практически все (и число овец в стаде, и число ступенек на египетской пирамиде, и т. д.) в этой жизни имеет что-то вроде особенной связи с числами и формулами. Хоть Бальмер был по образованию математик, он не внес значительного вклада в свою область, но оказал содействие дальнейшему развитию физики своей спектральной формулой для атома водорода.

Его достижение было по-настоящему выдающимся. В то время Бальмер знал только о четырех частотах в спектре атома водорода, которые экспериментально определил Андерс Ангстрем (1814–1874). Используя только эти четыре значения, Бальмер в шестьдесят лет составил формулу, предсказавшую полный спектр частот атома водорода (а также верно предсказавшую нижнюю и верхнюю границы диапазона частот). Вскоре после этого Бальмер узнал, что эта формула не только объяснила те четыре изначальных значения, но и правильно предсказала двенадцать других частот.

В 1885 году он опубликовал свои труды в двух статьях, которые сделали его имя бессмертным. За годы было определено еще больше спектральных частот, но формула Бальмера остается неизменной. В 1890 году Йоханнес Ридберг (1854–1919) обнаружил, что формула Бальмера на самом деле является частным случаем более общей формулы (которую сейчас мы называем формулой Ридберга ):

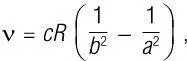
где ν — частота, c — скорость света, а R — постоянная Ридберга. Частоты Бальмера для атома водорода можно получить, если установить b = 2 и a = 3, 4, 5, 6 и т. д. Хотя эта формула правильно предсказала линии, наблюдаемые в спектре атома водорода, никто не знал, почему она работала — она просто работала. В течение еще тридцати лет атом держал это в тайне.

Следуя предложению Хансена, Бор взглянул на формулу Бальмера. Возможно, он увидел ее в общем варианте Ридберга (см. выше). Формула была хорошо известна, и, скорее всего, Бор увидел ее еще студентом, только чтобы потом забыть. Мы уже обсуждали то, как Бор предположил, что энергия связи электрона в атоме квантована подобно тому, как Планк проквантовал энергию резонаторов. Используя эту гипотезу с некоторой очень простой классической физикой, Бор смог получить общее выражение для разности энергий связи Δ E двух квантовых состояний с квантовыми числами n 1и n 2:

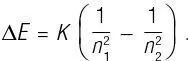
Снова увидев формулу Бальмера, Бор, должно быть, немедленно понял, как вытащить физику, все эти годы глубоко скрывавшуюся в этой формуле. А затем Бор выдвинул следующую гипотезу: что разность энергий квантовых состояний электрона равна энергии светового кванта Эйнштейна, h ν: