В. Макаровский: Взгляд на мироздание

Многомерная дельта-функция представляет собой бесконечно узкий многомерный импульс. На рис. 1 показан пример положительного и отрицательного одномерных белых спектров частот, а на рис. 2 – пример обратного преобразования этих спектров в пространственную форму. Обратное преобразование формирует положительную и отрицательную дельта-функции. Дельта-функция представляет собой бесконечно узкий импульс. Эти два рисунка демонстрируют возможность представления одного и того же процесса в двух формах: спектральной и пространственной.

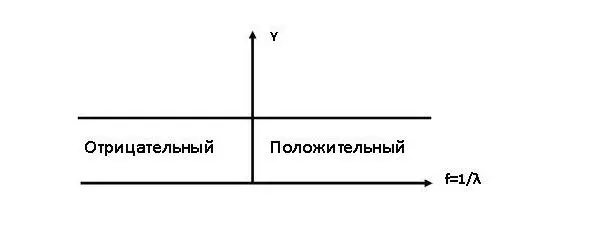
Рис.1. Пример белого одномерного спектра частот

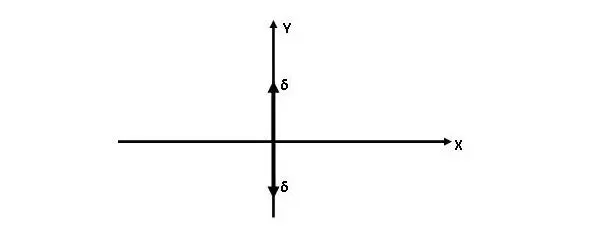
Рис.2. Пример обратного преобразования Фурье спектра рис.1

Для обработки процессов в спектральной форме создана теория фильтрации. Теория фильтрации описывает структуры фильтров и их характеристики. Каждый фильтр имеет вход, на который поступают входные сигналы, и выход, который выдает результат фильтрации. Входные и выходные сигналы фильтров представляют собой наборы вибраций разных частот. Важнейшими характеристиками фильтра являются амплитудно-частотная, импульсная и переходная. Амплитудно-частотная характеристика показывает: с каким весом проходят на выход фильтра колебания различных входных частот. Импульсная реакция показывает выходной сигнал фильтра при воздействии на его вход дельта-импульса. Переходная характеристика показывает выходной сигнал фильтра при воздействии на его вход ступенчатой функции. Импульсная и амплитудно-частотная характеристики связаны между собой парой преобразования Фурье. Импульсная и переходная характеристики связаны между собой дифференциальным и интегральным преобразованиями. Амплитудно-частотная характеристика обладает важным параметром – полосой пропускания частот; чем шире эта полоса, тем больший спектр частот проходит через фильтр. Переходная характеристика обладает протяженностью и переменной крутизной нарастания. Чем более растянута переходная характеристика фильтра, тем меньше полоса пропускания его амплитудно-частотной характеристики и наоборот. Чем выше крутизна переходной характеристики, тем выше крутизна реализации фильтруемого процесса, т. е. процесс быстрее нарастает или спадает. Любой фильтр представляет собой тот или иной вариант накопления колебаний, а каждый вариант соответствует строго определенным амплитудно-частотной и импульсной характеристикам. Обратное преобразования Фурье представляет собой фильтр с равномерной амплитудно-частотной характеристикой в бесконечной полосе частот. Еще раз подчеркнем, что в данной гипотезе рассматриваются пространственные координаты, пространственные колебания в этих координатах и совершенно не рассматривается понятие времени.

На рисунке 3 схематически показаны амплитудно-частотные характеристики трех фильтров нижних частот с разными полосами пропускания. Полоса пропускания частот фильтра С больше полосы пропускания частот фильтра В, которая, в свою очередь, больше полосы пропускания частот фильтра А. Частота ω –величина обратно пропорциональная длине волны λ.На рисунке 4 схематически показаны переходные характеристики этих фильтров. Из сопоставления этих рисунков видно, что чем шире полоса пропускания фильтра, тем круче нарастает его переходная характеристика.

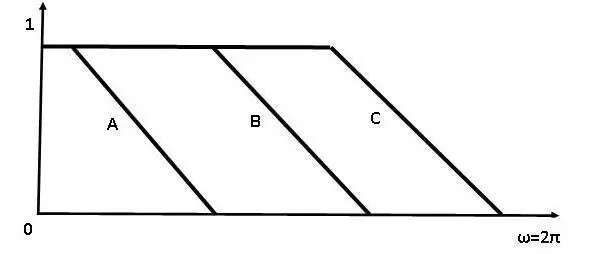
Рис.3. Амплитудно-частотные характеристики трех фильтров

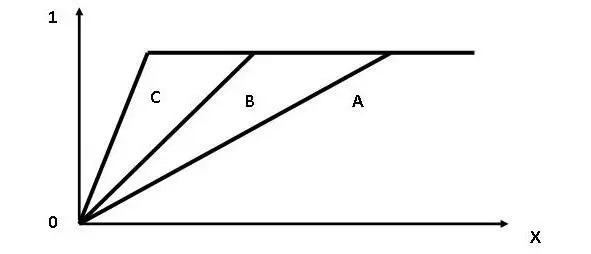
Рис.4. Переходные характеристики трех фильтров

С овокупность многомерных положительного и отрицательного спектров (положительного и отрицательного хаосов) содержит в себе практически неиссякаемые возможности для построения всех вещей и явлений мироздания. Аналогично, белый звуковой шум содержит в себе все возможные музыкальные произведения, нужно только должным образом этот шум профильтровать. Инструментальной базой проявления мироздания является процесс многомерной фильтрации спектра (хаоса) бесконечным множеством фильтров с бесконечным многообразием параметров как по всем nизмерениям, так и по любому другому сочетанию измерений. Процессы фильтрации являются основными, а возможно и единственными процессами, обеспечивающими проявление материального мироздания из исходного многомерного хаоса.