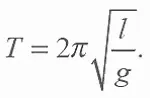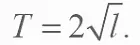Нурбей Гулиа - Удивительная физика

Если бы медведь был поумнее и отодвинулся бы в сторону, то чурбан совершал бы свои колебания сам по себе, свободно. Такие колебания назовем собственными колебаниями, а частоту их – собственной частотой, так как собственно сам чурбан их и создает. Постепенно эти колебания затухают, и их можно назвать затухающими. Но если медведь вновь примется толкать чурбан, вынуждая его увеличивать размах колебаний, то такие колебания справедливо назвать вынужденными. И если медведь окажется столь глупым, что будет толкать чурбан с частотой собственных колебаний, то размах будет все увеличиваться, пока не наступит катастрофа – падение медведя. Такой случай, когда частота возмущающей силы совпадает с частотой собственных колебаний, называется резонансом.

Вот мы и изучили физические причины, вызывающие колебания, а к тому же вспомнили основную терминологию, связанную с этим явлением.

Восстанавливающая сила может быть не только силой тяжести, как в нашем случае. Она может быть, например, и силой упругости, если бы чурбан был подвешен на пружинах. Многие силы могут быть восстанавливающими, лишь бы они восстанавливали равновесие.

Возвращаясь к нашему случаю с медведем, зададимся вопросом: а как выбирать длину веревки, на которой подвешен чурбан? Чем длиннее веревка, тем больше размах, но тем больше и время, через которое чурбан снова вернется к медведю и ударит его. Назовем это время периодом колебаний, так как возврат в исходное положение при колебаниях происходит не однократно, а периодически. Так вот если период будет слишком велик, то медведь успеет проскочить к меду, минуя удар чурбаном. Значит, длиной веревки, на которой подвешен чурбан, мы регулируем период колебаний. Чем длиннее веревка, тем больше период.

Но важно то, что этот период не зависит от размаха колебаний. Мала или велика, конечно, в определенных пределах, амплитуда колебаний маятника, период колебаний маятника зависит не от нее, а как мы установили, только от длины маятника. Даже сопротивление воздуха движению маятника существенно не влияет на период. И все это первым заметил Галилео Галилей. Он не был охотником на медведей. Просто будучи добрым католиком, Галилей много времени проводил в соборе, где помимо прочего наблюдал за колебаниями светильника на длинном подвесе (в православных храмах такой светильник называют паникадилом). Он, измеряя период колебаний биением своего пульса (наручных-то часов тогда не было!), и пришел к выводу, что ни масса подвешенного груза, ни амплитуда колебаний практически не влияют на период.

Это был очень важный вывод – на его основании впоследствии были изобретены точные маятниковые часы, и созданы они были великим голландским физиком Христианом Гюйгенсом (1629—1695). Но об этом потом. А пока нам важно знать, что Гюйгенс первым установил зависимость периода колебаний от длины маятника. Если груз на подвесе считать маленькой тяжелой точкой (такой маятник называется математическим), то период Т колебаний прямо пропорционален корню квадратному из длины маятника l. Если эти колебания происходят не на поверхности Земли, а на Луне например, или на высокой горе, или в глубокой шахте, то там ускорение силы тяжести отличается от того, к которому мы привыкли: g = 9,81 м/с 2. И тогда нам важно знать, что период колебаний обратно пропорционален корню квадратному из ускорения силы тяжести. Иначе говоря, формула Гюйгенса имеет вид:

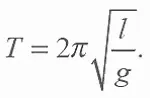
Сам автор для практических целей пользуется упрощенной формулой. Так как число π в квадрате очень близко к значению ускорения силы тяжести на уровне океана (т. е. не на высокой горе или в глубокой шахте), то формула упрощается и приобретает вид:

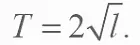
Если, например, длина маятника равна 1 м, то период колебаний равен 2 секундам: секунда – туда, секунда – обратно. Значит, имея часы, можно измерять длину. И наоборот, рулетка может стать измерителем времени, а часы – расстояния! Но удобнее, конечно, первый вариант.

Если задаваться необходимым периодом колебаний, то можно вычислить длину маятника по упрощенной формуле:

l = 0,25 T 2

Эта формула тут же подтверждает, что длина маятника с периодом 2 секунды равна 1 м. А интересно, каков будет маятник длиною в час? То есть чтобы период его был равен часу или 3 600 секундам? Подставляем и получаем: