Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

Фиг. 28. Демонстрация и анализ движения тела, находящегося под действием некоторой доли силы тяжести.

а— шар катится по наклонной плоскости; б— траектория движения шара, записанная на бумаге.

Шарик движется поперек и одновременно скатывается вниз по наклонной плоскости, оставляя след при движении (для этого использована копировальная бумага). Чтобы произвести анализ движения, изобразите на листе бумаги, на котором вычерчена траектория движения, прямые с координатами

x 2 = 2 x1, x 3 = 3 x 1

Измерьте y1, y2 и т. д. и проверьте, выполняются ли соотношения

y 2 = 2 2 y 1, y 2 = 3 2 y 1 и т. д.

* * *

На фиг. 26 показана фотография шарика, брошенного в воздух, полученная при помощи серии коротких световых вспышек, следующих через равные промежутки времени.

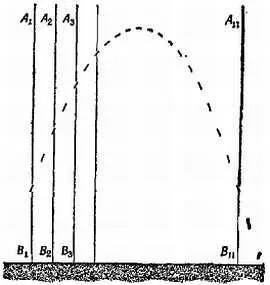
Фиг. 26. Траектория летящего тела, сфотографированного при помощи световых вспышек.

Произведите сами измерения по траектории на фотографии, проведя линии А 1 В 1, A 2 B 2, A 3 B 3. Вы увидите, что линии разделены равными промежутками: A 1 A 2= A 2 A 3=… Шарик поднимается по вертикали все медленнее и медленнее, а затем падает все быстрее и быстрее; в перемещении же по горизонтали он движется, не ускоряясь и не замедляясь. Горизонтальное движение летящего шарика остается неизменным.

Галилей знал об этом свойстве движущихся предметов и дал эти представления Ньютону. В течение многих столетий до него большинство ученых настаивало на том, что для поддержания постоянной скорости движения необходимо действие силы.

Это представление древних и сегодня находит отклик, если мы полагаемся на здравый смысл. Чтобы ящик двигался по полу, вам приходится его толкать; автомобиль, катящийся по горизонтальному участку пути, потребляет бензин, и двигатель каким-то образом создает постоянное усилие. Если вы оставите движущийся предмет в покое, говорили древние, то он остановится. Но для Галилея и Ньютона шероховатый пол и ветер не оставляют движущееся тело в покое: они создают силы, которые действуют на тело и препятствуют его движению (мы называем их силами трения или сопротивления воздуха). Массивное пушечное ядро, движущееся с небольшой скоростью, испытывает лишь незначительное сопротивление воздуха; оно почти предоставлено самому себе в отношении движения по горизонтали и сохраняет это движение.

Отсюда возникает новое представление о движении, согласно которому движению тела присуще нечто, что поддерживает его, пока тело не встречает противодействия. Это нечто было названо мыслителями XIV столетия в Париже и Оксфорде «импульсом». Их труды дошли до Леонардо да Винчи примерно в 1500 г., а до Галилея около 1600 г. и оказали на них влияние. Если бы существовало книгопечатание, то современные взгляды на движение, возможно, распространились бы еще за три столетия до Галилея.

Импульс — удобное название этого качества движущегося тела, имеющее в современном словаре оттенок значения «движущий вперед». Впоследствии мы изменим это название на термин «количество движения», которому мы придадим более точный смысл [28] В большинстве книг по физике оба термина импульс и количество движения используются на равных правах. — Прим. ред . . Обратите внимание, что ни одно из этих слов ничего не объясняет: это в лучшем случае этикетки, наводящие на мысль, напоминающие о том, что движущееся тело несет свое движение с собой и не нуждается для его поддержания в усилии. Слово «импульс» латинского происхождения, оно обозначает «движение».

Наблюдая за движением пушечного ядра, Галилей говорил, что пушка сообщает ядру импульс, который ядро сохраняет . Горизонтальная часть этого импульса остается неизменной. Вертикальная часть, или, как мы говорим, вертикальная составляющая, изменяется под действием силы тяжести, как и при движении любого другого падающего тела. Если к ящику нужно прилагать постоянное усилие, чтобы он продолжал двигаться по полу, то это значит, что пол создает силы, препятствующие движению, Галилей и Ньютон сказали бы, что нашего постоянного усилия, направленного вперед, как раз достаточно для противодействия этой тормозящей силе. И в этом случае, когда ящик движется с постоянной скоростью, действующая на него суммарная сила равна нулю. На фиг. 31 показана схема опыта, предназначенного для доказательства этого утверждения, однако в этом доказательстве скрыт один существенный дефект.