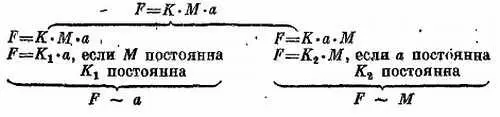Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

Если это покажется странным, воспользуйтесь криволинейной поверхностью собственного лба в качестве наклонной плоскости и прижмите к нему палец. Лоб будет отталкивать палец с силой, направленной прямо от поверхности, если не считать трения, которое вы сможете почувствовать. Попробуйте представить себе, что трение при этом отсутствует.

Если вы намерены стать осторожным физиком, избегайте пагубного слова «создает». Все, что мы на самом деле знаем, это то, что силы и ускорение сопутствуют друг другу. Во многих случаях не удается независимым образом показать, что действует сила, просто мы считаем, что сила действует, поскольку наблюдается ускорение.

Качение шара вносит одно осложнение, о котором мы умолчали, поэтому для исследования этой зависимости между силой и ускорением мы пользуемся скольжением тел по наклонной плоскости «без трения» или наблюдаем движение тележки по рельсам. В последнем случае тележка движется прямолинейно, и лишь ее колеса вращаются.

Предположим, у нас имеется несколько наклонных плоскостей одинаковой высоты h , но с разным наклоном, и движение по ним происходит без трения (фиг. 152).

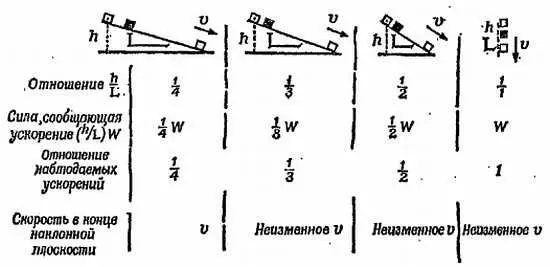
Фиг. 152.

Последим за скольжением какого-нибудь тела из состояния покоя в верхней точке каждой из наклонных плоскостей. Если ускорения пропорциональны h / L , можно предсказать, что во всех случаях тело к концу движения приобретет одну и ту же скорость v . Для равноускоренного движения из состояния покоя v 2= 2 as(см. гл. 1, приложение I ), и если a= C( h/ L), где С — постоянная, то v 2= 2 as= 2 C( h/ L)∙(Расстояние L) = 2 C∙ h, т. е. одинаково для всех наклонных плоскостей. Если же скорость v одинакова для всех наклонных плоскостей одной и той же высоты h , то ускорения должны быть пропорциональны отношению h / L . Галилей был убежден, что это свойство «одинаковой скорости» установлено им правильно, и во многих случаях пользовался им как отправной точкой при рассмотрении ускоренного движения.

Не так уж просто заметить, что зависимости F ~ а и F ~ М можно объединить В формулу F= K∙ M∙ а. Вспомним, что первые две формулировки содержат некоторые условия. Первая гласит: « F ~ апри неизменной массе М ». Но если М постоянна, то мы сможем записать более общую формулу F= K∙ M∙ а.

Таким образом,

F= (K∙ M)∙ а = (Постоянная)∙ а,

т. е. F ~ a .,

Следовательно, формула F= K∙ M∙ авключает утверждение « F~ a, если Мпостоянна ».

Второе утверждение гласит, что F ~ М , если ускорение а неизменно. Но если а остается неизменным, то мы можем записать формулу F= K∙ M∙ аследующим образом:

F= (K∙ M)∙ а = (Постоянная)∙ М,

т. е. F ~ M .

Следовательно, формула F= K∙ M∙ авключает зависимости F ~ а и F ~ M при определенных условиях:

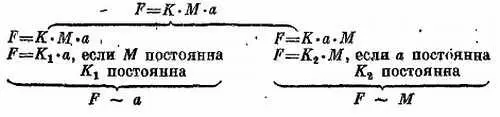
Для наших целей удобнее говорить, что масса — это отношение (сила)/(ускорение) ; это упрощает представление о незнакомой величине, какой является масса. Физики-специалисты обычно рассуждают как раз в обратном порядке. Они говорят, что масса представляет собой очевидную (!) меру тяжеловесности вещества (назвать это свойство вещества «инертностью» — значит просто присвоить ему некоторое наименование) и определяют силу как произведение (масса)∙(ускорение). Разумеется, это не устраняет сомнений с точки зрения логики, которые возникали в наших рассуждениях, а лишь «перемещает» их. Обе точки зрения могут быть приняты в качестве рабочих, но смешивать их было бы просто несовместимо с требованиями логики.

Рыба, пожалуй, сказала бы, что пузырьки воздуха поднимаются под действием силы плавучести, обусловленной земным отталкиванием.