Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

Доказательство Галилея было остроумным, но не вполне строгим. Суть его такова; сравним два перемещения, каждое из которых начинается из состояния покоя, — перемещение тела А на некоторое расстояние и перемещение тела В на вдвое большее расстояние. Если скорость возрастает пропорционально пройденному расстоянию, то скорости на соответствующих этапах перемещения В (половина пути, три четверти и т. д.) будут вдвое больше, чем при перемещении тела А . Значит, удвоенный путь телом В проходится с удвоенными скоростями и отнимает в целом столько же времени, сколько перемещение тела А , что абсурдно. Но это доказательство предполагает, что движение могло начаться из состояния покоя. Строгий вариант доказательства требует применения математического анализа, чтобы показать, что описанное движение никогда не может начаться из состояния покоя. Начавшись, такое движение продолжалось бы все более стремительно, и его скорость возрастала бы по закону сложных процентов.

Science for the Citizen, London, 1938.

В математическом анализе скорость vв данный момент определяется как первая производная пути по времени v = ds / dt , а ускорение а в данный момент — как первая производная скорости по времени, т, е. равно dv / dt , или d 2 s / dt 2(вторая производная пути по времени).

Из математического анализа следует, что если s = kt 2, то скорость ds / dt = 2 kt , а ускорение dv / dt = d / dt ( ds / dt ) = 2 k , т. е. постоянно.

Этот прибор был грубым. Галилей пользовался им скорее для подтверждения своего предположения, нежели для измерения ускорения.

Галилей убедился в том, что скорость, приобретаемая телом при скольжении по наклонной плоскости без трения, зависит только от высоты h , а не от длины наклонной плоскости L (фиг. 5). А если это так, то тело, свободно падающее по вертикали с высоты h , должно приобрести такую же скорость, ибо падение равносильно движению по вертикальной наклонной плоскости. Поэтому Галилей мог с уверенностью перейти от своих экспериментов к выводу о свободном падении.

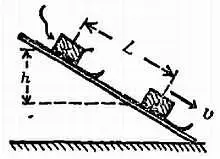
Фиг. 5. Движение из состояния покоя.

Смысл этой остроумной пословицы в ее обычном понимании не имеет отношения к данному случаю: «Если есть исключение, то должно быть и правило».

Опытный экспериментатор объединил бы обе таблицы, т. е. просто в табл. 1 оставил бы лишнюю колонку для «среднего времени». Если бы этот экспериментатор предвидел, что ему потребуется еще табл. 3, он оставил бы еще одну колонку для величины ( время ) 2. Даже если бы он не ждал, что ему потребуется что-то еще, он все же оставил бы пустые колонки и несколько свободных строк под строкой с цифрой 5,40 на тот случай, что впоследствии нужно будет записать что-то еще.

Можно произвести косвенную проверку, проводя на графике касательные. См. следующий раздел.

Имеем ли мы в виду «предполагать» или «надеяться»? Если «предполагать», то на каком основании, а если «надеяться», то научный ли это подход?

Например, если ускорение не постоянно, а быстро уменьшается до нуля от некоторого большого значения, то движущееся тело набирает скорость главным образом в самом начале своего перемещения. В этом случае средняя скорость больше ( v 0+ v )/2.

Если вы склонны посмеяться над этим древним представлением, то спросите своих друзей, как предложил Лойд Тайлор, какую траекторию вычерчивает современная винтовочная пуля непосредственно после вылета из ствола. Летит она по прямой или сразу же начинает падать?

В большинстве книг по физике оба термина импульс и количество движения используются на равных правах. — Прим. ред .

Для таких направленных расстояний принят технический термин «смещение».

В обиходном языке, говоря о скорости, имеют в виду, насколько быстро движется предмет по какой-либо траектории — прямолинейной или искривленной. В физике скорость — это перемещение за единицу времени в определенном направлении, представляющее собой вектор. Чтобы задать скорость, указывают число, единицу измерения и направление, например 15 км/час в северном направлении.