Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

2) Накопление знаний . Научные достижения XVII века значительны и многообразны: к ним следует отнести законы Кеплера, открытие кометы Галлея, закон Гука, открытие Гарвеем системы кровообращения, открытия Бойля в области химии и его закон для идеальных газов.

3) Достижения в области математики. Была изобретена декартова система координат. Графики связали алгебру с геометрией, с одной стороны, сводя геометрические формы и преобразования к сжатым алгебраическим выражениям, а с другой — позволяя наглядно представлять алгебраические уравнения.

На графике I фиг. 98 изображена проходящая через начало координат прямая линия, на которой нанесены точки ( x 1, y 1), ( x 2, y 2)…. Из подобия треугольников следует, что отношения y 1/ x 1, y 2/ x 2…. равны между собой, т. е. одинаковы для любой точки на прямой. Обозначим эту постоянную k . Тогда каждая точка на прямой будет представлена парой значений (например, x 1, y 1), удовлетворяющих соотношению у / х = k или у = kх . Это и есть алгебраическое описание графика, а прямая представляет собой геометрический образ данного соотношения. Если у и х — результаты физических измерений (например, s и t 2для падающего тела), то прямая линия выражает соотношение y = (const) x , или у ~ х , а наклон прямой определяет постоянную.

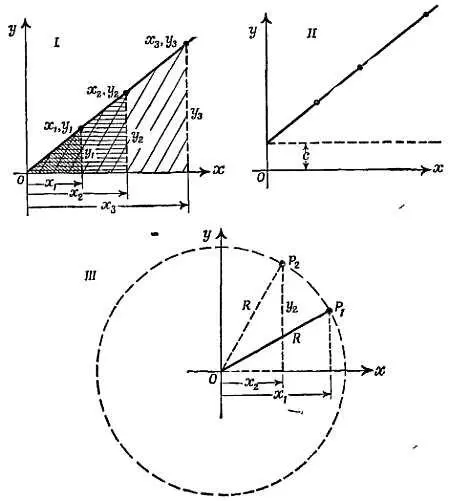
Фиг. 98. Графики в декартовой системе координат.

График II иллюстрирует уравнение у= k х+ с. В этом случае мы не можем сказать, что у ~ х , но можем сказать, что Δ у ~ Δх .

На графике III изображена окружность, причем

для точки P 1

x 2 1+ у 2 1= R 2

для точки P 2

x 2 2+ у 2 2= R 2

таким образом, уравнение этой окружности имеет вид

x 2+ у 2= R 2

Его можно переписать так:

x 2/ R 2+ y 2/ R 2= 1

Эллипс можно получить равномерным растяжением окружности.

Нарисуйте окружность на листе резины и растяните этот лист (фиг. 99).

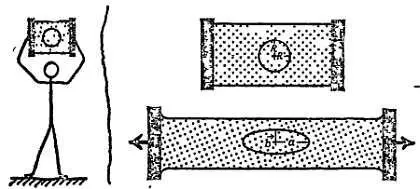
Фиг. 99. Растяжение окружности в эллипс.

Радиус R превратится в полуоси а и b . Окружность в соответствии о уравнением x 2/ R 2+ y 2/ R 2= 1 и с площадью круга π R 2= π∙ R∙ Rпревратится в эллипс, описываемый уравнением…?.. = 1 и площадью =?

Таким образом, с помощью декартовой геометрии эллиптические орбиты можно записать в виде алгебраических уравнений.

Возникли две серьезные математические проблемы, связанные с вычислениями: определение угла наклона касательных к кривым и площадей под кривыми с помощью математики , т. е. создание методов дифференцирования и интегрирования . Тангенс угла наклона касательной определяет скорость изменения функции. Вычисления сводятся просто к нахождению скорости изменения функции в некоторой точке. Это позволяет нам вычислять ускорения из выражения, описывающего изменение скорости , или скорости из выражения, связывающего расстояние и время . (Например: если s= 16 t 2, то v= 32 t; отсюда следует, что а= 32, т. е. постоянное значение.) Интегрирование — операция сложения бесконечно большого числа бесконечно малых величин: нахождение площади путем сложения элементов исчезающе малых размеров (как и в случае второго закона Кеплера) или нахождение силы притяжения между телами конечных размеров путем суммирования сил притяжения бесконечно малых элементов объема этих тел.

Вы уже пользовались графиками и вычислениями ранее, при решении задачи о колесе, катящемся вниз с холма.

1. ЭКСПЕРИМЕНТ —> ГРАФИК. Вы наносите на график зависимость s от t 2. Точки изображают события . Проведенная через эти точки прямая представляет собой совокупность фактов.

2. РАЗМЫШЛЕНИЯ —> ТЕОРИЯ. Предположите, что ускорение постоянно, рассматривая это как возможный простой закон природы. Вычислите необходимое соотношение между s и t . При интегрировании будут складываться все маленькие расстояния, проходимые с возрастающей скоростью; при этом получится, что при постоянном ускорении s должно меняться пропорционально t 2.