Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

РАССТОЯНИЕ, ПРОХОДИМОЕ ТЕЛОМ ИЗ СОСТОЯНИЯ ПОКОЯ, ПРОПОРЦИОНАЛЬНО КВАДРАТУ ВРЕМЕНИ.

Неизвестно, действительно ли Галилей сам произвел этот опыт или просто описал опыт, произведенный еще до него. Как бы то ни было, измерения были грубые, хотя Галилей считал, что установил правильный «закон». С помощью остроумных геометрических доказательств он показал, что этому закону должно с необходимостью подчиняться движение с постоянным соотношением Δ v /Δ t .

Таким образом, катящийся шар движется с постоянным ускорением. С помощью экстраполяции, переходя от малого наклона к большему и, наконец, к падению по вертикали, Галилей доказал, что свободно падающие тела имеют постоянное ускорение; следовательно, он получил закон, которому подчиняется их падение.

На произвольной наклонной плоскости сила, вызывающая ускорение, должна быть одинакова на всем пути. (Это — постоянная составляющая веса шара.) Таким образом, Галилей уже получил часть второго закона Ньютона: постоянная сила вызывает постоянное ускорение .

Рассматривая холмы с различными склонами, Галилей почти вплотную подошел к главному соотношению второго закона Ньютона: ускорение пропорционально силе ; но это соотношение он выражал в геометрической форме, что не позволяло выявить роль силы. Галилей разработал экспериментальные методы науки о движении, которыми можно было пользоваться при решении самых разнообразных задач: о полете снарядов, движении маятников, планет, а позднее о движении различных механизмов и даже составных частей атомов.

Скорость у подножия холма

Галилей пришел к такому выводу: если шар катится вниз с одной наклонной плоскости А, а затем вверх по другой наклонной плоскости В, то он докатится до первоначального уровня, каков бы ни был наклон. Это привело его к очень важному общему допущению, на основании которого он сделал много предсказаний. Вообразим себе несколько различных склонов А 1, A 2, A 3 одной и той же высоты , примыкающих к склону В (фиг. 88).

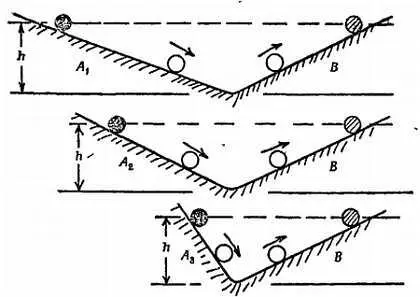
Фиг. 88. Идеальный случай движения «с горки на горку».

Если предположение Галилея правильно, то шар должен подняться на одну и ту же высоту по склону В, независимо от того, с какого склона А он спустился. У подножия холма, перед тем, как шар начнет подниматься по склону В , он будет иметь импульс, необходимый для того, чтобы подняться на склон В до точки, соответствующей той же высоте. Этот импульс должен, следовательно, быть одним и тем же у подножия холмов А 1, A 2и т. д., т. е. одним и тем же для всех склонов. Поэтому шар должен иметь одну и ту же скорость у подножия любого склона. Галилей сделал на основании этого общее предположение: скорости, приобретаемые телом, движущимся по плоскостям, имеющим различные наклоны, равны между собой, если равны высоты, с которых он спускается. Мы вкратце говорили об этом свойстве в гл. 7 [62] Гл. 7 « Сила и движение » входит в т. 1 настоящего-издания. , где указывали, что оно относится ко второму закону Ньютона. Галилей обобщил этот вывод на случай холмов, имеющих неровные склоны. Используя приведенные рассуждения и постоянство ускорения, Галилей получил ряд геометрических следствий для движения тел по наклонной плоскости.

Правило «с горки на горку»

Успешной демонстрации опыта с шаром, скатывающимся вниз по одному склону и затем подымающемуся вверх по другому на ту же высоту, препятствует трение. В своих рассуждениях Галилей, вероятно, исходил не только из эксперимента, но и из теоретических соображений — он обладал гениальной интуицией и благодаря ей, опираясь на самые грубые эксперименты, выдвигал правильные гипотезы. Для своих коллег Галилей подкреплял гипотезу тщательными аргументами о сложных движениях вниз и вверх, так что гипотеза должна была представляться еще более правдоподобной. Рассмотрим следующий «мысленный эксперимент» Галилея (описанный позже другим автором). Предположим, что шар остановится на склоне В выше . Воспользуемся доской С (фиг. 89, а ), заставим шар скатиться обратно к началу его движения по склону А и позволим ему снова скатиться со скоростью, которую он приобрел. Будем повторять этот процесс. Шар от раза к разу будет приобретать все больший и больший импульс, что является абсурдом. Если шар, поднимаясь по склону В , остановится ниже , мы должны будем производить отсчет от (…нечитаемый текст…)такой подход к решению различных проблем имели большое значение. Кроме того, здесь, как и в любой другой области физики, дискуссия могла помочь выяснению данной проблемы, указать путь, по которому следует вести исследование.