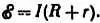Исследования зависимости силы тока от напряжения приводят к открытию важного закона. Подавляющее большинство проводников подчиняется закону:
U= I∙ R.
Величине R можно дать название сопротивления, в полном соответствии с начальными качественными наблюдениями. Читателю знакома запись: это закон Ома. Подставляя значение силы тока из выражений закона Ома в предыдущую формулу, мы находим:
Q= ( U 2/ R)∙ τ
Надеюсь, что вас не спутает возможность записать выражение энергии, выделяемой проводником в форме тепла, и иначе:
Q= I 2∙ R∙ τ.
Из первой формулы следует, что количество тепла обратно пропорционально сопротивлению. Говоря эту фразу, надо добавить: при неизменном напряжении. Именно этот случай мы и имели в виду, когда впервые воспользовались термином «сопротивление». А вот вторая формула, утверждающая, что тепло прямо пропорционально сопротивлению, требует, чтобы вы добавили: при постоянной силе тока.
В написанных выражениях читатель узнает закон, который носит имена Джоуля и Ленца.
Выяснив, что напряжение и сила тока пропорциональны, и получив, таким образом, возможность определять сопротивление проводника, исследователь естественно задается вопросом, как связана эта важная величина с формой и размером проводника и с веществом, из которого он сделан.
Опыты приводят к следующему открытию. Оказывается, что
R= ρ∙ l/ S ,
где l — длина проводника, a S — его поперечное сечение. Это простейшее выражение справедливо тогда, когда мы имеем дело с линейным проводником неизменного сечения по всей своей длине. При желании, прибегнув к более сложным математическим операциям, можно записать формулу сопротивления для проводника любой формы. Ну, а что это за коэффициент ρ? Он характеризует материал, из которого изготовлен проводник. Значение этой величины, которая получила название удельного сопротивления, колеблется в очень больших пределах. По величинам ρ вещества могут отличаться в миллиарды раз.
Проделаем еще несколько формальных преобразований, которые пригодятся в дальнейшем. Закон Ома можно записать в такой форме:
I= U∙ S/ρ∙ l
Приходится часто встречаться с отношением силы тока к площади сечения проводника. Его называют плотностью тока и обозначают обычно буквой j . Теперь тот же закон запишется так:
j = (1/ρ)∙( U/ l)
Исследователю кажется, что с законом Ома ему все ясно. Располагая неограниченным количеством проводников, сопротивление которых известно, можно отказаться от громоздких определений напряжения с помощью калориметра: напряжение ведь равно произведению силы тока — на сопротивление.
Однако ученый быстро находит, что это утверждение нуждается в уточнении. Используя один и тот же источник тока, он замыкает его полюса различными сопротивлениями. Сила тока, естественно, при каждом опыте будет разной. Но оказывается, что и произведение силы тока на сопротивление I ∙ R не остается одним и тем же. Занявшись изучением этого, пока что непонятного, явления, исследователь обнаруживает, что по мере увеличения сопротивления произведение I ∙ R стремится к некоторой постоянной величине.
Обозначив этот предел через 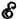 мы находим формулу, не совпадающую с той, которая была установлена прямыми измерениями силы, тока и напряжения. Новая формула имеет вид:
мы находим формулу, не совпадающую с той, которая была установлена прямыми измерениями силы, тока и напряжения. Новая формула имеет вид:
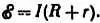
Что 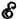 странное противоречие?
странное противоречие?
Приходится подумать. Ну, конечно, противоречие кажущееся. Ведь непосредственное измерение напряжения калориметрическим способом относилось только к проводу, замыкающему аккумулятор. А ведь ясно, что тепло выделяется и в самом аккумуляторе (для того, чтобы в этом убедиться, достаточно дотронуться до аккумулятора рукой). Аккумулятор обладает своим сопротивлением. Смысл величины r , стоящей в новой формуле, очевиден: это внутреннее сопротивление источника тока. Что же касается величины то для нее нужно особое название. Нельзя сказать, что выбор был особенно удачным: величину 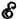 называют электродвижущей силой (ЭДС), хотя она не имеет ни смысла, ни размерности силы.
называют электродвижущей силой (ЭДС), хотя она не имеет ни смысла, ни размерности силы.
Читать дальше

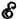 мы находим формулу, не совпадающую с той, которая была установлена прямыми измерениями силы, тока и напряжения. Новая формула имеет вид:
мы находим формулу, не совпадающую с той, которая была установлена прямыми измерениями силы, тока и напряжения. Новая формула имеет вид: