Итак, звезда даже в самый большой телескоп не может быть, как говорят астрономы, «разрешена». Это означает, что мы можем измерять только потоки излучения от звезд в разных спектральных участках. Мерой величины потока является видимая звездная величина, определение которой предполагается известным (см., например, книгу: П. И. Бакулин, Э. В. Кононович и В. И. Мороз, «Курс общей астрономии»). Полезно только напомнить, что самые слабые из наблюдаемых звезд имеют видимую величину m = 24, в то время как самая яркая звезда Сириус имеет звездную величину -1 , 6. Зная разность звездных величин двух звезд, можно найти отношение потоков от них F 1 /F 2, если воспользоваться простой формулой:
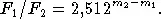 |
(1.1) |
Полезно еще знать, что Солнце имеет визуальную звездную величину m  = -26 , 73. В то же время прямые измерения дают значение потока солнечного излучения в абсолютных единицах, равное
= -26 , 73. В то же время прямые измерения дают значение потока солнечного излучения в абсолютных единицах, равное
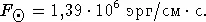
Эта величина носит название «солнечной постоянной». Не представляет труда по известной видимой величине какой-нибудь звезды, цвет которой такой же, как у Солнца, оценить величину ее потока в абсолютных (энергетических) единицах. Допустим, что видимая величина звезды m = 20. Тогда по формуле (1.1) получим, что логарифм отношения потока от этой звезды к потоку от Солнца будет равен
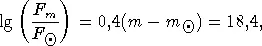
откуда F m  10 -12эрг/см 3
10 -12эрг/см 3  с.
с.
Если мы теперь каким-нибудь образом знаем расстояние до звезды r , то очевидно, что полная мощность ее излучения (или «светимость») может быть получена из простой формулы:
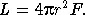 |
(1.2) |
Если, в нашем примере, расстояние до звезды равно 100 парсек (1 парсек (пс) = 3 , 26 светового года = 3  10 18см), то ее светимость будет L = 10 30эрг/с. Полезно запомнить, что светимость Солнца L
10 18см), то ее светимость будет L = 10 30эрг/с. Полезно запомнить, что светимость Солнца L  = 4
= 4  10 33эрг/с. Таким образом, наша звезда излучает в несколько тысяч раз слабее Солнца — это, как говорят, «карликовая» звезда. Из формулы (1.2) следует очевидное обстоятельство, что при данной светимости поток излучения от звезды обратно пропорционален квадрату расстояния до нее. Таким образом, видимая величина определяется, с одной стороны, светимостью звезды,— с другой стороны,— расстоянием до нее. Одной и той же видимой величине может соответствовать сравнительно близко находящаяся звезда низкой светимости (карлик) или удаленная звезда высокой светимости (гигант). Поэтому характеристикой светимости звезды является ее абсолютная величина , обычно обозначаемая буквой M . Это та величина, которую имела бы интересующая нас звезда, если бы расстояние до нее было равно стандартному значению 10 парсек. Между видимой и абсолютной величинами имеется простое соотношение:
10 33эрг/с. Таким образом, наша звезда излучает в несколько тысяч раз слабее Солнца — это, как говорят, «карликовая» звезда. Из формулы (1.2) следует очевидное обстоятельство, что при данной светимости поток излучения от звезды обратно пропорционален квадрату расстояния до нее. Таким образом, видимая величина определяется, с одной стороны, светимостью звезды,— с другой стороны,— расстоянием до нее. Одной и той же видимой величине может соответствовать сравнительно близко находящаяся звезда низкой светимости (карлик) или удаленная звезда высокой светимости (гигант). Поэтому характеристикой светимости звезды является ее абсолютная величина , обычно обозначаемая буквой M . Это та величина, которую имела бы интересующая нас звезда, если бы расстояние до нее было равно стандартному значению 10 парсек. Между видимой и абсолютной величинами имеется простое соотношение:
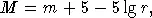 |
(1.3) |
где r выражено в парсеках.
Таким образом, одна из основных характеристик звезды — светимость— определяется, если известна видимая величина и расстояние до нее. Если для определения видимой величины астрономия располагает вполне надежными методами, то расстояния до звезд определить не так просто. Для сравнительно близких звезд, удаленных на расстояние, не превышающее нескольких десятков парсек, расстояния определяются известным еще с начала прошлого столетия тригонометрическим методом, заключающимся в измерении ничтожно малых угловых смещений звезд при их наблюдении с разных точек земной орбиты, т. е. в разное время года. Этот метод дает наибольшую точность и очень надежен. Однако для огромного большинства более удаленных звезд он уже не годится: слишком малые смещения положения звезды надо измерять — меньше сотой доли секунды дуги! На помощь приходят другие методы, значительно менее точные, но тем не менее достаточно надежные. В ряде случаев абсолютную величину звезд можно определить и непосредственно, без измерения расстояния до них, по некоторым наблюдаемым особенностям их излучения. На всех этих методах мы, конечно, останавливаться здесь не можем и отсылаем интересующихся читателей к специальным руководствам, например, к содержательной книге Ю. Н. Ефремова «В глубины Вселенной» («Наука», 1977). Вообще, проблема определения расстояния до удаленных космических объектов (звезд, туманностей, галактик) всегда была и сейчас остается одной из центральных в астрономии.
Читать дальше

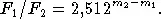
 = -26 , 73. В то же время прямые измерения дают значение потока солнечного излучения в абсолютных единицах, равное
= -26 , 73. В то же время прямые измерения дают значение потока солнечного излучения в абсолютных единицах, равное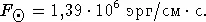
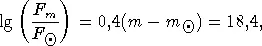
 10 -12эрг/см 3
10 -12эрг/см 3  с.
с.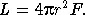
 10 18см), то ее светимость будет L = 10 30эрг/с. Полезно запомнить, что светимость Солнца L
10 18см), то ее светимость будет L = 10 30эрг/с. Полезно запомнить, что светимость Солнца L  = 4
= 4  10 33эрг/с. Таким образом, наша звезда излучает в несколько тысяч раз слабее Солнца — это, как говорят, «карликовая» звезда. Из формулы (1.2) следует очевидное обстоятельство, что при данной светимости поток излучения от звезды обратно пропорционален квадрату расстояния до нее. Таким образом, видимая величина определяется, с одной стороны, светимостью звезды,— с другой стороны,— расстоянием до нее. Одной и той же видимой величине может соответствовать сравнительно близко находящаяся звезда низкой светимости (карлик) или удаленная звезда высокой светимости (гигант). Поэтому характеристикой светимости звезды является ее абсолютная величина , обычно обозначаемая буквой M . Это та величина, которую имела бы интересующая нас звезда, если бы расстояние до нее было равно стандартному значению 10 парсек. Между видимой и абсолютной величинами имеется простое соотношение:
10 33эрг/с. Таким образом, наша звезда излучает в несколько тысяч раз слабее Солнца — это, как говорят, «карликовая» звезда. Из формулы (1.2) следует очевидное обстоятельство, что при данной светимости поток излучения от звезды обратно пропорционален квадрату расстояния до нее. Таким образом, видимая величина определяется, с одной стороны, светимостью звезды,— с другой стороны,— расстоянием до нее. Одной и той же видимой величине может соответствовать сравнительно близко находящаяся звезда низкой светимости (карлик) или удаленная звезда высокой светимости (гигант). Поэтому характеристикой светимости звезды является ее абсолютная величина , обычно обозначаемая буквой M . Это та величина, которую имела бы интересующая нас звезда, если бы расстояние до нее было равно стандартному значению 10 парсек. Между видимой и абсолютной величинами имеется простое соотношение: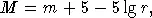





![Андрэ Нортон - Рожденные среди звезд [= Рождение звезды]](/books/322400/andre-norton-rozhdennye-sredi-zvezd-rozhdenie-zve-thumb.webp)
![Эдвард Радзинский - Тираны России и СССР [Распутин. Жизнь и смерть + Сталин. Жизнь и смерть]](/books/391099/edvard-radzinskij-tirany-rossii-i-sssr-rasputin-thumb.webp)


