Обратим теперь внимание на то, что в поле тяготения регистрирующие приборы могут измерять только относительные ускорения, т. е. разность ускорений в двух точках. Относительное ускорение от точечного или сферически-симметричного тела меняется с расстоянием как 1 /r 3 — это хорошо известное выражение для приливных сил. Квадрупольная составляющая гравитации от системы тел или несимметричного тела вызывает относительное ускорение, равное  GMa 2 l/r 5, где l — расстояние между двумя пробными частицами. Мы видим, что это относительное ускорение очень быстро убывает с расстоянием.
GMa 2 l/r 5, где l — расстояние между двумя пробными частицами. Мы видим, что это относительное ускорение очень быстро убывает с расстоянием.
Релятивистская теория тяготения в этом пункте радикально расходится с ньютоновской. Согласно общей теории относительности для r > ct (где t — характерное время изменения квадрупольного момента, например, период орбитального движения двойной системы звезд или период осевого вращения несимметричного тела), относительное ускорение, обусловленное квадрупольным моментом, меняется не как r -5, а как r -1. При этом, если изменение со временем квадрупольного момента носит периодический характер, фаза этих относительных ускорений смещена на величину r/cr . Все это означает, что меняющийся со временем квадрупольный момент гравитирующего тела (или системы тел) создает на больших расстояниях специфическое гравитационное поле, имеющее характер распространяющейся со скоростью света волны . Можно показать, что гравитационные волны поперечны и поляризованы .
Принципиальное различие между эйнштейновской и ньютоновской теорией тяготения ярко выявляется на примере кеплеровского движения в двойной звездной системе. Согласно классической теории Ньютона такая система (если считать, что звезды имеют «точечные» размеры) сколь угодно долго сохраняет свою энергию. Наоборот, согласно теории тяготения Эйнштейна такая система должна непрерывно терять энергию на излучение гравитационных волн. Этот эффект особенно силен для тесных двойных систем (см. § 22, где речь шла о возможности объяснения пульсаров системами двойных нейтронных звезд). На достаточно больших расстояниях от двойной системы относительное ускорение, обусловленное гравитационной волной, на много порядков превосходит обычное приливное «статическое» ускорение, создаваемое такой системой, которое убывает как r -3.
Какие же космические объекты являются источниками гравитационного излучения? Прежде всего — это тесные двойные (или кратные) системы. Усредненная по периоду обращения мощность гравитационного излучения от двойной системы дается формулой
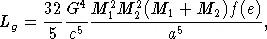 |
(24.7) |
причем частота гравитационного излучения равна удвоенной частоте орбитального движения (т.е. 4  /T , где T — период системы), M 1и M 2 — массы компонент, a — большая полуось орбиты, f ( e ) — некоторая функция эксцентриситета орбиты e , меняющаяся с ростом e от 1 до весьма больших значений. По этой формуле можно найти, что мощность гравитационного излучения Юпитера, движущегося по своей орбите, L g = 5
/T , где T — период системы), M 1и M 2 — массы компонент, a — большая полуось орбиты, f ( e ) — некоторая функция эксцентриситета орбиты e , меняющаяся с ростом e от 1 до весьма больших значений. По этой формуле можно найти, что мощность гравитационного излучения Юпитера, движущегося по своей орбите, L g = 5  10 10эрг/с — величина совершенно ничтожная (
10 10эрг/с — величина совершенно ничтожная (  5 киловатт — всего лишь!). Однако у тесных двойных систем мощность гравитационного излучения несравненно больше. У некоторых систем (например, UV Льва) она доходит до 2
5 киловатт — всего лишь!). Однако у тесных двойных систем мощность гравитационного излучения несравненно больше. У некоторых систем (например, UV Льва) она доходит до 2  10 32эрг/с, что составляет 5% от светимости Солнца. Потоки гравитационного излучения от ближайших к нам таких звездных систем доходят до 10 -10эрг/см 2
10 32эрг/с, что составляет 5% от светимости Солнца. Потоки гравитационного излучения от ближайших к нам таких звездных систем доходят до 10 -10эрг/см 2  с. Это близко к потоку световой энергии от звезды 15-й видимой величины. Полный поток гравитационного излучения на Земле от всех звезд в Галактике должен быть около 10 -9эрг/см 2
с. Это близко к потоку световой энергии от звезды 15-й видимой величины. Полный поток гравитационного излучения на Земле от всех звезд в Галактике должен быть около 10 -9эрг/см 2  с, причем частота этого излучения, определяемая средними орбитальными периодами, порядка 10 -4с -1.
с, причем частота этого излучения, определяемая средними орбитальными периодами, порядка 10 -4с -1.
Другим источником гравитационного излучения являются вращающиеся вокруг своих осей звезды с несимметричным распределением массы (например, трехосные эллипсоиды). Мощность гравитационного излучения- такой звезды определяется формулой (22.3) (см. § 22).
Читать дальше

 GMa 2 l/r 5, где l — расстояние между двумя пробными частицами. Мы видим, что это относительное ускорение очень быстро убывает с расстоянием.
GMa 2 l/r 5, где l — расстояние между двумя пробными частицами. Мы видим, что это относительное ускорение очень быстро убывает с расстоянием.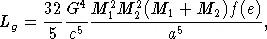
 /T , где T — период системы), M 1и M 2 — массы компонент, a — большая полуось орбиты, f ( e ) — некоторая функция эксцентриситета орбиты e , меняющаяся с ростом e от 1 до весьма больших значений. По этой формуле можно найти, что мощность гравитационного излучения Юпитера, движущегося по своей орбите, L g = 5
/T , где T — период системы), M 1и M 2 — массы компонент, a — большая полуось орбиты, f ( e ) — некоторая функция эксцентриситета орбиты e , меняющаяся с ростом e от 1 до весьма больших значений. По этой формуле можно найти, что мощность гравитационного излучения Юпитера, движущегося по своей орбите, L g = 5  10 10эрг/с — величина совершенно ничтожная (
10 10эрг/с — величина совершенно ничтожная (  5 киловатт — всего лишь!). Однако у тесных двойных систем мощность гравитационного излучения несравненно больше. У некоторых систем (например, UV Льва) она доходит до 2
5 киловатт — всего лишь!). Однако у тесных двойных систем мощность гравитационного излучения несравненно больше. У некоторых систем (например, UV Льва) она доходит до 2  10 32эрг/с, что составляет 5% от светимости Солнца. Потоки гравитационного излучения от ближайших к нам таких звездных систем доходят до 10 -10эрг/см 2
10 32эрг/с, что составляет 5% от светимости Солнца. Потоки гравитационного излучения от ближайших к нам таких звездных систем доходят до 10 -10эрг/см 2  с. Это близко к потоку световой энергии от звезды 15-й видимой величины. Полный поток гравитационного излучения на Земле от всех звезд в Галактике должен быть около 10 -9эрг/см 2
с. Это близко к потоку световой энергии от звезды 15-й видимой величины. Полный поток гравитационного излучения на Земле от всех звезд в Галактике должен быть около 10 -9эрг/см 2  с, причем частота этого излучения, определяемая средними орбитальными периодами, порядка 10 -4с -1.
с, причем частота этого излучения, определяемая средними орбитальными периодами, порядка 10 -4с -1.




![Андрэ Нортон - Рожденные среди звезд [= Рождение звезды]](/books/322400/andre-norton-rozhdennye-sredi-zvezd-rozhdenie-zve-thumb.webp)
![Эдвард Радзинский - Тираны России и СССР [Распутин. Жизнь и смерть + Сталин. Жизнь и смерть]](/books/391099/edvard-radzinskij-tirany-rossii-i-sssr-rasputin-thumb.webp)


