Открытие космического радиоизлучения коренным образом изменило старую проблему обнаружения дисперсии электромагнитных волн в межзвездной среде. Последнюю всегда можно рассматривать как плазму (даже в «зонах Н I», где водород не ионизован; см. § 2). Теория распространения и дисперсии радиоволн в плазме является очень хорошо разработанным отделом макроскопической физики. Приведем только выражение для показателя преломления электромагнитных волн в плазме, в которой магнитное поле отсутствует:
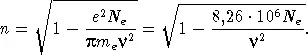 |
(21.1) |
Здесь N e — концентрация свободных электронов в плазме, 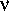 — частота излучения.
— частота излучения.
Как видно из формулы (21.1), показатель преломления плазмы для радиоволн меньше единицы. Как известно из элементарного курса физики, скорость распространения электромагнитных волн в среде с показателем преломления n 3 ф= c/n , где c = 3  10 10см/с — скорость света в вакууме. Коль скоро n меньше единицы, 3 ф > c , что как будто бы противоречит специальному принципу относительности. Никакого противоречия, однако, здесь нет. Дело в том, что 3 фесть так называемая «фазовая скорость», относящаяся к строго определенной частоте волны. Принцип относительности утверждает, что нельзя передавать сигналы со сверхсветовой скоростью. Однако при помощи так называемой «монохроматической волны» (т. е. волны со строго определенной частотой) никакого сигнала передать нельзя. Для этого надо пользоваться группой волн , частоты которых слегка различны. Такая группа волн (или «волновой пакет») распространяется в среде с некоторой групповой скоростью, которая отличается от фазовой. В случае распространения волн в достаточно разреженной плазме групповая скорость выражается формулой
10 10см/с — скорость света в вакууме. Коль скоро n меньше единицы, 3 ф > c , что как будто бы противоречит специальному принципу относительности. Никакого противоречия, однако, здесь нет. Дело в том, что 3 фесть так называемая «фазовая скорость», относящаяся к строго определенной частоте волны. Принцип относительности утверждает, что нельзя передавать сигналы со сверхсветовой скоростью. Однако при помощи так называемой «монохроматической волны» (т. е. волны со строго определенной частотой) никакого сигнала передать нельзя. Для этого надо пользоваться группой волн , частоты которых слегка различны. Такая группа волн (или «волновой пакет») распространяется в среде с некоторой групповой скоростью, которая отличается от фазовой. В случае распространения волн в достаточно разреженной плазме групповая скорость выражается формулой
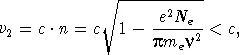 |
(21.2) |
а время распространения группы волн
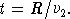
Из этих формул следует, что разница времени распространения группы волн в среде (плазме) и в вакууме (т. е. запаздывание группы ) будет равна
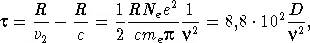 |
(21.3) |
где величина D = N e R — число свободных электронов в цилиндре, площадь основания которого равна одному квадратному сантиметру, а образующая равна R . В формуле (21.3) частота 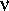 выражена в мегагерцах, a R — в парсеках. Величина D называется «мерой дисперсии». Допустим теперь, что измеряется время приходов импульсов на двух частотах, слегка различающихся одна от другой на величину
выражена в мегагерцах, a R — в парсеках. Величина D называется «мерой дисперсии». Допустим теперь, что измеряется время приходов импульсов на двух частотах, слегка различающихся одна от другой на величину 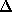
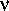 . Подчеркнем, что импульс радиоизлучения, содержащий набор частот, был испущен в некоторый момент времени и если бы не дисперсия межзвездной среды, он наблюдался бы одновременно на всех частотах. Наличие же дисперсии приводит к тому, что на более высоких частотах импульс будет наблюдаться раньше, чем на низких. Разница в моментах времени наблюдения импульса на частотах, различающихся на величину
. Подчеркнем, что импульс радиоизлучения, содержащий набор частот, был испущен в некоторый момент времени и если бы не дисперсия межзвездной среды, он наблюдался бы одновременно на всех частотах. Наличие же дисперсии приводит к тому, что на более высоких частотах импульс будет наблюдаться раньше, чем на низких. Разница в моментах времени наблюдения импульса на частотах, различающихся на величину 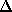 t , как можно показать, будет равна
t , как можно показать, будет равна
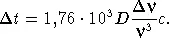 |
(21.4) |
Чтобы почувствовать, велика ли эта величина или мала, сделаем численный расчет. Допустим, что 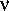 = 100 МГц, a D = 100 см -3
= 100 МГц, a D = 100 см -3  пс. Тогда из формулы (21.4) следует, что при
пс. Тогда из формулы (21.4) следует, что при 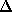
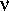 = 1 МГц
= 1 МГц 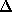 t
t  1 с! Это очень большая величина, особенно если учесть, что 1 секунда близка к среднему периоду пульсаров. Из этого примера видно, что межзвездная дисперсия радиосигналов от пульсаров очень сильно искажает наблюдаемую структуру импульсов. В отдельных случаях, если не принять особых мер (например, не сузить полосу частот, которую принимает приемник радиоизлучения), она может «замыть» импульсы и сделать их ненаблюдаемыми. Об искажении наблюдений пульсаров межзвездной дисперсией мы уже говорили раньше.
1 с! Это очень большая величина, особенно если учесть, что 1 секунда близка к среднему периоду пульсаров. Из этого примера видно, что межзвездная дисперсия радиосигналов от пульсаров очень сильно искажает наблюдаемую структуру импульсов. В отдельных случаях, если не принять особых мер (например, не сузить полосу частот, которую принимает приемник радиоизлучения), она может «замыть» импульсы и сделать их ненаблюдаемыми. Об искажении наблюдений пульсаров межзвездной дисперсией мы уже говорили раньше.
Читать дальше

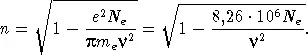
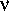 — частота излучения.
— частота излучения. 10 10см/с — скорость света в вакууме. Коль скоро n меньше единицы, 3 ф > c , что как будто бы противоречит специальному принципу относительности. Никакого противоречия, однако, здесь нет. Дело в том, что 3 фесть так называемая «фазовая скорость», относящаяся к строго определенной частоте волны. Принцип относительности утверждает, что нельзя передавать сигналы со сверхсветовой скоростью. Однако при помощи так называемой «монохроматической волны» (т. е. волны со строго определенной частотой) никакого сигнала передать нельзя. Для этого надо пользоваться группой волн , частоты которых слегка различны. Такая группа волн (или «волновой пакет») распространяется в среде с некоторой групповой скоростью, которая отличается от фазовой. В случае распространения волн в достаточно разреженной плазме групповая скорость выражается формулой
10 10см/с — скорость света в вакууме. Коль скоро n меньше единицы, 3 ф > c , что как будто бы противоречит специальному принципу относительности. Никакого противоречия, однако, здесь нет. Дело в том, что 3 фесть так называемая «фазовая скорость», относящаяся к строго определенной частоте волны. Принцип относительности утверждает, что нельзя передавать сигналы со сверхсветовой скоростью. Однако при помощи так называемой «монохроматической волны» (т. е. волны со строго определенной частотой) никакого сигнала передать нельзя. Для этого надо пользоваться группой волн , частоты которых слегка различны. Такая группа волн (или «волновой пакет») распространяется в среде с некоторой групповой скоростью, которая отличается от фазовой. В случае распространения волн в достаточно разреженной плазме групповая скорость выражается формулой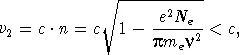
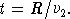
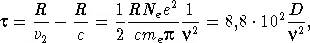
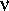 выражена в мегагерцах, a R — в парсеках. Величина D называется «мерой дисперсии». Допустим теперь, что измеряется время приходов импульсов на двух частотах, слегка различающихся одна от другой на величину
выражена в мегагерцах, a R — в парсеках. Величина D называется «мерой дисперсии». Допустим теперь, что измеряется время приходов импульсов на двух частотах, слегка различающихся одна от другой на величину 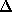
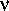 . Подчеркнем, что импульс радиоизлучения, содержащий набор частот, был испущен в некоторый момент времени и если бы не дисперсия межзвездной среды, он наблюдался бы одновременно на всех частотах. Наличие же дисперсии приводит к тому, что на более высоких частотах импульс будет наблюдаться раньше, чем на низких. Разница в моментах времени наблюдения импульса на частотах, различающихся на величину
. Подчеркнем, что импульс радиоизлучения, содержащий набор частот, был испущен в некоторый момент времени и если бы не дисперсия межзвездной среды, он наблюдался бы одновременно на всех частотах. Наличие же дисперсии приводит к тому, что на более высоких частотах импульс будет наблюдаться раньше, чем на низких. Разница в моментах времени наблюдения импульса на частотах, различающихся на величину 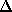 t , как можно показать, будет равна
t , как можно показать, будет равна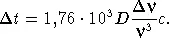
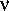 = 100 МГц, a D = 100 см -3
= 100 МГц, a D = 100 см -3  пс. Тогда из формулы (21.4) следует, что при
пс. Тогда из формулы (21.4) следует, что при 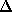
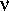 = 1 МГц
= 1 МГц 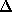 t
t  1 с! Это очень большая величина, особенно если учесть, что 1 секунда близка к среднему периоду пульсаров. Из этого примера видно, что межзвездная дисперсия радиосигналов от пульсаров очень сильно искажает наблюдаемую структуру импульсов. В отдельных случаях, если не принять особых мер (например, не сузить полосу частот, которую принимает приемник радиоизлучения), она может «замыть» импульсы и сделать их ненаблюдаемыми. Об искажении наблюдений пульсаров межзвездной дисперсией мы уже говорили раньше.
1 с! Это очень большая величина, особенно если учесть, что 1 секунда близка к среднему периоду пульсаров. Из этого примера видно, что межзвездная дисперсия радиосигналов от пульсаров очень сильно искажает наблюдаемую структуру импульсов. В отдельных случаях, если не принять особых мер (например, не сузить полосу частот, которую принимает приемник радиоизлучения), она может «замыть» импульсы и сделать их ненаблюдаемыми. Об искажении наблюдений пульсаров межзвездной дисперсией мы уже говорили раньше.




![Андрэ Нортон - Рожденные среди звезд [= Рождение звезды]](/books/322400/andre-norton-rozhdennye-sredi-zvezd-rozhdenie-zve-thumb.webp)
![Эдвард Радзинский - Тираны России и СССР [Распутин. Жизнь и смерть + Сталин. Жизнь и смерть]](/books/391099/edvard-radzinskij-tirany-rossii-i-sssr-rasputin-thumb.webp)


