Стивен Хокинг - Мир в ореховой скорлупе

В 1931 г. Курт Гёдель доказал знаменитую теорему о природе математики. Эта теорема утверждает, что в любой формальной системе аксиом вроде тех, что используются в современной математике, всегда существуют положения, которые не могут быть ни доказаны, ни опровергнуты на основе аксиом, определяющих систему.

Теорема Гёделя наложила фундаментальное ограничение на математику. Она стала настоящим шоком для научного сообщества, поскольку заставила отбросить широко распространенное убеждение, будто математика является согласованной и полной системой, основанной исключительно на логическом фундаменте. Теорема Гёделя, принцип неопределенности Гейзенберга и практическая невозможность проследить эволюцию даже детерминированных систем, когда они становятся хаотическими, составляют ядро набора ограничений, наложенных на научное знание, смысл которых в полной мере был осознан только в XX веке.

Космические струны не следует путать с элементарными объектами теории струн, с которыми они совершенно не связаны. Подобные объекты имеют протяженность, но при этом обладают крохотным поперечным сечением. Их существование предсказывается в некоторых теориях элементарных частиц. Пространство-время за пределами одиночной космической струны плоское. Однако это плоское пространство-время имеет клинообразный вырез, вершина которого лежит как раз на струне. Оно похоже на конус: возьмите большой круг из бумаги и вырежьте из него сектор, подобный куску пирога, вершина которого расположена в центре круга. Удалив вырезанный кусок, склейте края разреза у оставшейся части — получится конус. Он изображает пространство-время, в котором существует космическая струна (рис. 5.5).

Заметьте, поскольку поверхность конуса — это все тот же плоский лист бумаги, с которого мы начали (за вычетом удаленного сектора), его можно по-прежнему считать плоским, за исключением вершины. Наличие кривизны в вершине можно выявить по тому факту, что описанные вокруг нее окружности имеют меньшую длину, чем окружности, удаленные на такое же расстояние от центра на исходном круглом листе бумаги. Иными словами, окружность вокруг вершины короче, чем должна быть окружность того же радиуса в плоском пространстве из-за отсутствующего сектора (рис. 5.6).

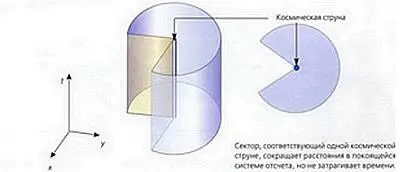
Рис. 5.6.Космическая струна вырезает сектор из пространства-времени

Подобным же образом удаленный из плоского пространства-времени сектор укорачивает окружности вокруг космической струны, но не влияет на время или расстояние вдоль нее. Это означает, что пространство-время вокруг отдельной космической струны не содержит временных петель, и, следовательно, путешествия в прошлое невозможны. Однако если есть вторая космическая струна, которая движется относительно первой, ее направление времени будет комбинацией времени и пространственных изменений первой. Это значит, что сектор, который вырезается второй струной, будет сокращать как расстояния в пространстве, так и интервалы времени для наблюдателя, который движется вместе с первой струной (рис. 5.7).

Если струны движутся друг относительно друга с околосветовой скоростью, сокращение времени при обходе обеих струн может быть столь значительным, что вы вернетесь обратно раньше, чем стартуете. Другими словами, здесь имеются временные петли, по которым можно путешествовать в прошлое.

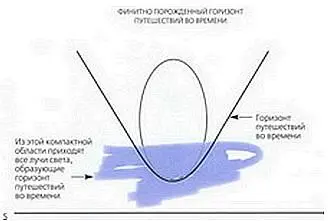
Даже самая могущественная цивилизация может искривить пространство-время только в конечной (финитной) области. Горизонт путешествий во времени — граница той части пространства-времени, в которой можно путешествовать в чье-то прошлое, — должен быть образован лучами света, исходящими из этой финитной области.

Космические струны содержат материю, обладающую положительной плотностью энергии, что совместимо с известной на сегодня физикой. Однако скручивание пространства, которое порождает временные петли, тянется до самой бесконечности в пространстве и до бесконечного прошлого во времени. Так что подобные структуры пространства-времени изначально, по построению допускают возможность путешествий во времени.