Stephen Hawking - The Grand Design

This idea leads to a view of the universe that is profoundly different from the traditional concept, requiring us to adjust the way that we think about the history of the universe. In order to make predictions in cosmology, we need to calculate the probabilities of different states of the entire universe at the present time. In physics one normally assumes some initial state for a system and evolves it forward in time employing the relevant mathematical equations. Given the state of a system at one time, one tries to calculate the probability that the system will be in some different state at a later time. The usual assumption in cosmology is that the universe has a single definite history. One can use the laws of physics to calculate how this history develops with time. We call this the “bottom-up” approach to cosmology. But since we must take into account the quantum nature of the universe as expressed by the Feynman sum over histories, the probability amplitude that the universe is now in a particular state is arrived at by adding up the contributions from all the histories that satisfy the no-boundary condition and end in the state in question. In cosmology, in other words, one shouldn’t follow the history of the universe from the bottom up because that assumes there’s a single history, with a well-defined starting point and evolution. Instead, one should trace the histories from the top down, backward from the present time. Some histories will be more probable than others, and the sum will normally be dominated by a single history that starts with the creation of the universe and culminates in the state under consideration. But there will be different histories for different possible states of the universe at the present time. This leads to a radically different view of cosmology, and the relation between cause and effect. The histories that contribute to the Feynman sum don’t have an independent existence, but depend on what is being measured. We create history by our observation, rather than history creating us.

The idea that the universe does not have a unique observer-independent history might seem to conflict with certain facts we know. There might be one history in which the moon is made of Roquefort cheese. But we have observed that the moon is not made of cheese, which is bad news for mice. Hence histories in which the moon is made of cheese do not contribute to the present state of our universe, though they might contribute to others. That might sound like science fiction, but it isn’t.

An important implication of the top-down approach is that the apparent laws of nature depend on the history of the universe. Many scientists believe there exists a single theory that explains those laws as well as nature’s physical constants, such as the mass of the electron or the dimensionality of space-time. But top-down cosmology dictates that the apparent laws of nature are different for different histories.

Consider the apparent dimension of the universe. According to M-theory, space-time has ten space dimensions and one time dimension. The idea is that seven of the space dimensions are curled up so small that we don’t notice them, leaving us with the illusion that all that exist are the three remaining large dimensions we are familiar with. One of the central open questions in M-theory is: Why, in our universe, aren’t there more large dimensions, and why are any dimensions curled up?

Many people would like to believe that there is some mechanism that causes all but three of the space dimensions to curl up spontaneously. Alternatively, maybe all dimensions started small, but for some understandable reason three space dimensions expanded and the rest did not. It seems, however, that there is no dynamical reason for the universe to appear four-dimensional. Instead, top-down cosmology predicts that the number of large space dimensions is not fixed by any principle of physics. There will be a quantum probability amplitude for every number of large space dimensions from zero to ten. The Feynman sum allows for all of these, for every possible history for the universe, but the observation that our universe has three large space dimensions selects out the subclass of histories that have the property that is being observed. In other words, the quantum probability that the universe has more or less than three large space dimensions is irrelevant because we have already determined that we are in a universe with three large space dimensions. So as long as the probability amplitude for three large space dimensions is not exactly zero, it doesn’t matter how small it is compared with the probability amplitude for other numbers of dimensions. It would be like asking for the probability amplitude that the present pope is Chinese. We know that he is German, even though the probability that he is Chinese is higher because there are more Chinese than there are Germans. Similarly, we know our universe exhibits three large space dimensions, and so even though other numbers of large space dimensions may have a greater probability amplitude, we are interested only in histories with three.

What about the curled-up dimensions? Recall that in M-theory the precise shape of the remaining curled-up dimensions, the internal space, determines both the values of physical quantities such as the charge on the electron and the nature of the interactions between elementary particles, that is, the forces of nature. Things would have worked out neatly if M-theory had allowed just one shape for the curled dimensions, or perhaps a few, all but one of which might have been ruled out by some means, leaving us with just one possibility for the apparent laws of nature. Instead, there are probability amplitudes for perhaps as many as 10 500different internal spaces, each leading to different laws and values for the physical constants.

If one builds the history of the universe from the bottom up, there is no reason the universe should end up with the internal space for the particle interactions that we actually observe, the standard model (of elementary particle interactions). But in the top-down approach we accept that universes exist with all possible internal spaces. In some universes electrons have the weight of golf balls and the force of gravity is stronger than that of magnetism. In ours, the standard model, with all its parameters, applies. One can calculate the probability amplitude for the internal space that leads to the standard model on the basis of the no-boundary condition. As with the probability of there being a universe with three large space dimensions, it doesn’t matter how small this amplitude is relative to other possibilities because we already observed that the standard model describes our universe.

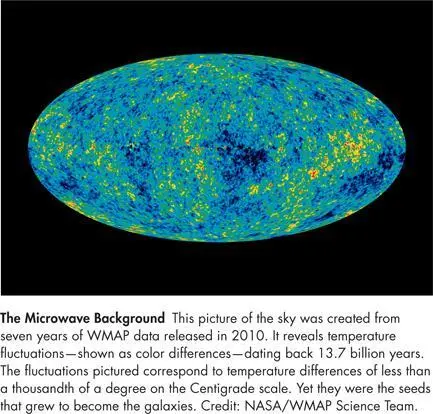
The theory we describe in this chapter is testable. In the prior examples we emphasized that the relative probability amplitudes for radically different universes, such as those with a different number of large space dimensions, don’t matter. The relative probability amplitudes for neighboring (i.e., similar) universes, however, are important. The no-boundary condition implies that the probability amplitude is highest for histories in which the universe starts out completely smooth. The amplitude is reduced for universes that are more irregular. This means that the early universe would have been almost smooth, but with small irregularities. As we’ve noted, we can observe these irregularities as small variations in the microwaves coming from different directions in the sky. They have been found to agree exactly with the general demands of inflation theory; however, more precise measurements are needed to fully differentiate the top-down theory from others, and to either support or refute it. These may well be carried out by satellites in the future.