Андрей Гришаев - Этот «цифровой» физический мир

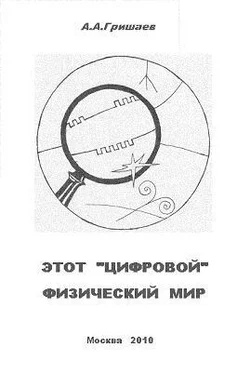
E=hf , (1.4.1)

где h - постоянная Планка. Не следует путать формулу (1.4.1) с аналогичной формулой, которая, как считается, описывает энергию фотона – притом, что до сих пор не дан чёткий ответ на вопрос о том, что же в фотоне колеблется. Ниже мы приведём ряд свидетельств о том, что фотонов – в традиционном понимании – не существует ( 3.10). Сейчас же мы говорим не о фотонах, а о веществе: мы утверждаем, что формула (1.4.1) описывает собственную энергию элементарной частицы вещества.

Собственную энергию элементарной частицы описывает ещё одна формула – эйнштейновская, которую называют «формулой ХХ века»:

E=mc 2, (1.4.2)

где m - масса частицы, c - скорость света. Комбинация формул (1.4.1) и (1.4.2) даёт формулу Луи де Бройля:

hf= mc 2. (1.4.3)

Смысл, который мы усматриваем в этой формуле, заключается в том, что три характеристики квантового пульсатора – собственная энергия, частота квантовых пульсаций и масса – прямо пропорциональны друг другу, будучи связаны через фундаментальные константы, а, значит, эти три характеристики представляют собой, в сущности, одно и то же физическое свойство . Отсюда естественным образом вытекает непротиворечивое и однозначное определение массы: масса элементарной частицы – это, с точностью до множителя c 2, энергия квантовых пульсаций этой частицы. Подчеркнём, что, при таком подходе, масса эквивалентна одной-единственной форме энергии – а именно, энергии квантовых пульсаций. Все остальные формы энергии не проявляют свойств массы – вопреки эйнштейновскому подходу, в котором любая энергия эквивалентна массе. Универсальность эйнштейновского подхода, как выясняется, неприемлема, поскольку из-за неё физика оказалась в тупике – до сих пор не умея объяснить, например, происхождения дефекта масс у составных ядер. А разгадка этой тайны, как мы постараемся показать, проста ( 4.7): часть собственной энергии связуемых нуклонов превращается в энергию их связи, которая свойств массы уже не проявляет.

Формула де Бройля (1.4.3) настолько фундаментальна, что, на наш взгляд, именно она является «формулой ХХ века», а не её кастрированный эйнштейновский вариант (1.4.2). Печально, но де Бройль признал ошибочность своей формулы – его убедили в том, что она релятивистски неинвариантна! Ведь специальная теория относительности (СТО) утверждает, что, по мере роста скорости частицы, масса испытывает релятивистский рост, а частота, наоборот, уменьшается из-за релятивистского замедления времени. Де Бройль, увы, не знал, что свидетельства о релятивистском росте массы были лживы с самого начала ( 4.5) – быстрый электрон слабее отклоняется магнитным полем не из-за увеличения массы электрона, а из-за уменьшения эффективности магнитного воздействия. Свидетельств же о релятивистском замедлении времени де Бройлю не предъявили – их ещё не было. Позднее такие свидетельства появились, но мы знаем, что они тоже являются лживыми ( 1.12-1.15) – в них желаемое выдаётся за действительное. Ни релятивистского роста массы, ни релятивистского замедления времени не существует в природе – поэтому, что бы ни происходило с частицей, соотношение (1.4.3) всегда остаётся справедливо! Например, для электрона, справочное значение массы покоя которого составляет 9.11·10 -31кг, соотношение (1.4.3) даёт частоту квантовых пульсаций, равную 1.24·10 20Гц.

Заметим, что, в отличие от официальной науки, которая более чем за сотню лет так и не объяснила природу собственной энергии (1.4.2), мы такое объяснение даём: собственная энергия частицы – это энергия её квантовых пульсаций!

Завершая это краткое знакомство с квантовым пульсатором, добавим, что он имеет характерный пространственный размер, который мы определяем как произведение периода квантовых пульсаций на скорость света. Используя (1.4.3), легко видеть, что введённый таким образом пространственный размер у частицы, имеющей массу m , равен её комптоновской длине: λ C= h /( mc ). У покоящегося электрона эта длина составляет 0.024 Ангстрема.

Следует, конечно, уточнить – что такое «покоящийся» электрон, что такое масса «покоя» электрона. По отношению к какой системе отсчёта следует говорить о покое или движении электрона? Ведь систем отсчёта много, и скорости одного и того же электрона по отношению к ним различны – а выше мы объявили однозначность состояний физических систем одним из главных физических принципов. Дело ведь не только в том, что, по отношению к наблюдателю Васе, скорость у электрона одна, а, по отношению к наблюдателю Пете – другая. Дело ещё и в том, что разным скоростям соответствуют разные кинетические энергии. А кинетическая энергия электрона должна быть однозначна – в согласии с законом сохранения и превращения энергии. Мы не будем уподобляться теоретикам, которые допускают любые душе угодные нарушения этого закона. Мы этот закон признаём и ставим во главу угла. Поэтому мы обязаны разъяснить, что такое «истинная-однозначная» скорость физического объекта, и как её правильно отсчитывать. Этот вопрос разбирается в 1.6.