Андрей Гришаев - Этот «цифровой» физический мир

Официальная теория гласит: вблизи устойчивой точки либрации «выведенное из равновесия» тело должно совершать эллиптические колебания вокруг этой точки [С4]. Каковы же размеры области устойчивости, в пределах которой возможны эти эллиптические колебания? По логике методов возмущений, отношение характерного размера области устойчивости к характерному расстоянию в данной задаче, т.е. к радиусу орбиты Юпитера, должно быть малым параметром, много меньшим единицы. В действительности же, разброс положений Троянцев грандиозен. На Рис.2.10 приведена карта положений малых тел Солнечной системы на 27 января 2006 г., в проекции на плоскость эклиптики; рисунок заимствован с общедоступного ресурса [ВЕБ12].

Здесь астероиды главного пояса обозначены малыми зелёными точками. Орбиту Юпитера изображает внешняя окружность; Юпитер, обозначенный кружком с крестиком, находится в точке, соответствующей примерно семи с половиной часам на циферблате; Троянцы изображены синими точками; центры их групп соответствуют примерно девяти с половиной и пяти с половиной часам. План выполнен с сохранением масштабов, и, как можно видеть, размеры «облаков» Троянцев сравнимы с радиусом орбиты Юпитера – вопреки теоретическим ожиданиям. Более того: чётко видно, что вытянутые вдоль орбиты Юпитера «облака» Троянцев изогнуты в соответствии с кривизной этой орбиты – словно, начиная с некоторой амплитуды, колебания Троянцев происходят по «изогнутым эллипсам»!

Таким образом, модель колебаний Троянцев около устойчивых точек либрации приводит к абсурду. Ключом же к разумному объяснению феномена является факт совпадения периодов «колебаний» Троянцев с периодом обращения их и Юпитера вокруг

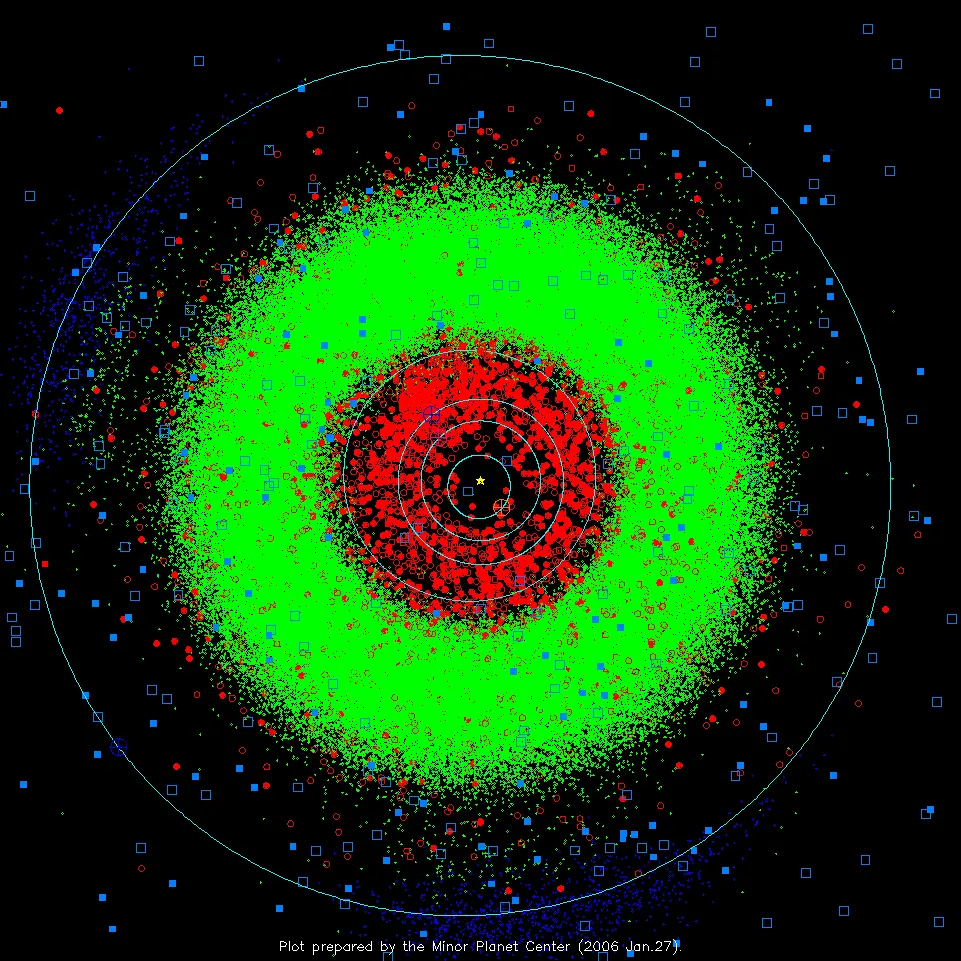
Рис.2.10

Солнца. Этот факт допускает совсем простую интерпретацию: Троянцы всего лишь движутся вокруг Солнца по эллиптическим орбитам с большими полуосями, равными большой полуоси орбиты Юпитера – тогда периоды их обращения такие же, как и у Юпитера. И ещё их орбиты имеют некоторый разброс по степени эллиптичности, т.е. разброс эксцентриситетов. Чем больше разница эксцентриситетов орбиты Троянца и орбиты Юпитера, тем больше размах углового сближения-расхождения того и другого – с периодом, равным периоду их обращения. Можно, конечно, продолжать валять дурака и полагать, что Троянцы «колеблются» - в чудовищных по размерам «областях устойчивости» и с чудовищным по длительности периодом. Но такие колебания, по всем теоретическим раскладам, должны быть чудовищно нелинейными. А у нелинейных колебаний, как назло, период зависит от амплитуды. Чего в случае Троянцев не наблюдается!

Но почему Троянцы оказываются сосредоточены лишь на двух зафиксированных по отношению к Юпитеру участках его орбиты? Мы рассмотрели такую задачу: частотная воронка Юпитера не достаёт до скоплений Троянцев, и они движутся, тяготея только к центру частотной воронки Солнца – положение которой изменяется из-за её «обращения», в противофазе с обращением Юпитера, около их барицентра. При таких условиях, обращение астероида, долговременно-синхронное с обращением Юпитера, возможно лишь при двух средних углах отстояния астероида от Юпитера, как раз ±60 о[Г8] – в согласии с опытом. И это при том, ещё раз отметим, что тяготение Юпитера на Троянец не действует!

Более того, подход [Г8] позволяет прояснить сценарий, по которому пополняются скопления Троянцев Юпитера. В эти скопления попадают астероиды из главного пояса, которым удаётся избежать «сметающего» действия частотной воронки Юпитера [Г8].

О каком «сметающем» действии речь? Да взгляните ещё раз на Рис.2.10 . Слишком бросается в глаза выраженная резкость внешнего и внутреннего краёв главного пояса астероидов. Официальная наука оставляет без комментариев этот поразительный факт – ибо ей и сказать-то нечего. Мы же этот факт легко объясняем: изнутри пояса, астероиды «подчищаются» частотной воронкой Марса, а снаружи – частотной воронкой Юпитера. Представьте: летел астероид, притягиваясь только к Солнцу, и вдруг он попадает в область планетарного тяготения. Скачком изменяется его локально-абсолютная скорость, бывшая эллиптическая траектория становится гиперболической… Короче, в области планетарного тяготения, такой астероид совершает пролётный «гравитационный манёвр», уводящий его с прежней околосолнечной орбиты. Такие же гравитационные манёвры с некоторых пор лихо закладывают управленцы полётами дальних космических зондов. Только эти управленцы помалкивают про то, что границы областей планетарного тяготения – резко выражены. А мы – ещё раз бросим взгляд на Рис.2.10 . Вот же они – свидетельства о границах!