После этого, массовый интерес к зонду HAYABUSA угас, и мало-помалу страсти улеглись. Спустя год, провели даже научную конференцию по тематике HAYABUSA-Итокава. Среди всего прочего, там демонстрировалась гравиметрическая карта астероида. Сам видел – редкой красоты вещь! Выполнена в традициях дзен; оказывает успокаивающее и расслабляющее действие. Созерцая этот шедевр, ни за что не подумаешь, что болванки без движков рядом с астероидом не удерживались!
2.6. Малые планеты: как же они ускоряются к Солнцу?
Из закона всемирного тяготения следует, что притяжение к нескольким массивным телам равно векторной сумме притяжений к каждому из них по отдельности. Т.е., тяготения нескольких тел действуют совместно, аддитивно. Такой подход приводит к поразительному парадоксу; мы изложим его в терминах гравитационных потенциалов.
Тело, имеющее собственное тяготение, находится в центре своей потенциальной ямы. Быть в яме означает быть в устойчивом равновесии. Отчего же малое тело, находясь вблизи много большего тела, ускоряется к нему? Оттого, говорят нам, что потенциальная ямка малого тела, складываясь с потенциальным склоном большого тела, возмущает этот склон настолько слабо, что суммарное распределение потенциала в объёме малого тела представляет собой, в первом приближении, склон, а не ямку – а по склону тело должно «скатываться». Очень хорошо! Теперь пусть малое тело удаляется всё дальше от большого. При этом крутизна потенциального склона большого тела становится всё меньше, и, наконец, она сравняется с крутизной потенциальной ямки малого тела на его поверхности. Расстояние от большого тела, на котором это произойдёт, мы называем дальностью отчуждения. За пределами дальности отчуждения малое тело находится уже не «на склоне», а «в ямке». Конечно, эта «ямка» асимметрична из-за перекоса, наводимого склоном большого тела – но теперь это, в первом приближении, ямка, а не склон. А в ямке тело должно удерживаться. С чего ему теперь «скатываться» в сторону большого тела? В перекошенной ямке у тела будет другое положение равновесия и другое распределение деформаций, чем в симметричной ямке, но перекошенная ямка будет удерживать тело не хуже, чем симметричная. Таким образом, из универсальности действия тяготения следует вывод: малое тело, находящееся за пределами дальности отчуждения от большого тела, не должно к нему ускоряться. Но практика не подтверждает этот вывод.
Действительно, для малого тела с массой m и радиусом r , дальность отчуждения D от от большого тела с массой M есть
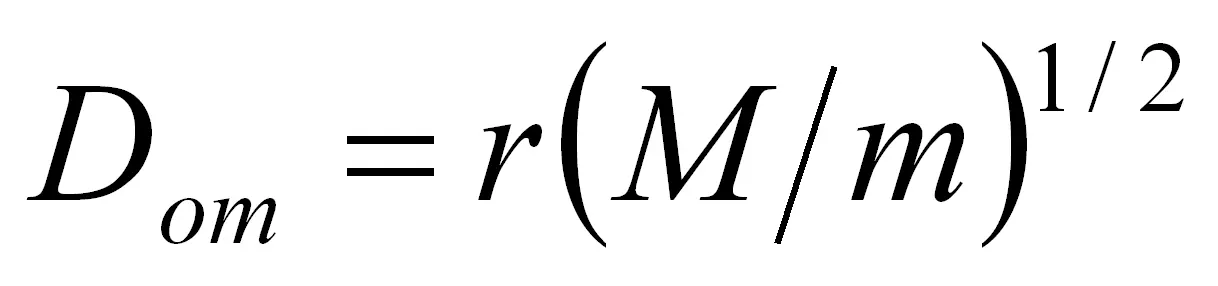 .
.
В таблице приведены рассчитанные по этой формуле дальности отчуждения от Солнца для некоторых малых планет ( a – расстояние от Солнца в афелии; справочные данные взяты из [К2]).

Как можно видеть, расстояния от Солнца, на которых малые планеты, несомненно, ускоряются к нему, на порядок превосходят соответствующие дальности отчуждения. Как такое возможно? Парадокс легко разрешался бы, если у малых планет, действительно, не было бы собственного тяготения, т.е. не было бы своих потенциальных ямочек. Тогда для них не было бы и дальностей отчуждения от Солнца, и они могли бы ускоряться к нему в пределах всей области действия солнечного тяготения – что и происходит в действительности.
2.7. Частотные склоны, как причина тяготения. Скорость действия тяготения.
Выше мы привели ряд примеров, которые свидетельствуют о том, что вещество не обладает способностью порождать тяготение. Оно не притягивает, оно лишь подчиняется тяготению. К чему же оно тяготеет? В такой форме – «К чему?» - вопрос некорректен. Правильнее спросить: «Куда направлено силовое воздействие?» Тогда ответ таков: «Оно направлено вниз по местной вертикали». А эти местные вертикали заданы чисто программными средствами.
Как мы излагали в 1.6, частоты квантовых пульсаций заданы программно. Если частота квантовых пульсаций, например, электрона, была бы задана одинаковой во всём пространстве, то такое пространство было бы «плоское», и в таком мире не было бы тяготения. Но программы, порождающие тяготение, обязывают частоты квантовых пульсаторов зависеть от местоположения в пространстве. Таким образом формируется программная реальность, которую мы называем частотными склонами. В области пространства, в которой «действует» частотный склон, в каждом месте задан локальный градиент частот квантовых пульсаций.
Читать дальше
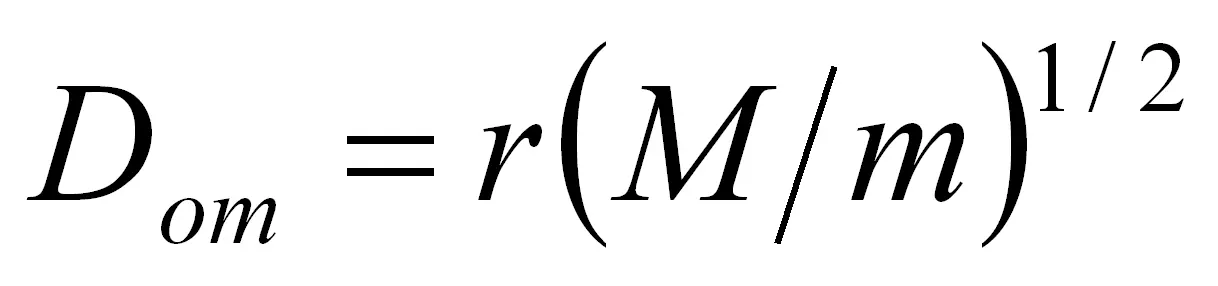 .
.











