Андрей Гришаев - Этот «цифровой» физический мир

Обратите внимание: энергия аннигиляционного гамма-кванта, 511 кэВ, в точности соответствует массе электрона (или позитрона). Такой квант мог бы порождаться при соединении электрона и позитрона в предельно связанную пару ( 4.7), когда дефект масс у каждого составляет 50%. Тогда, при «аннигиляции», электрон и позитрон не исчезали бы полностью – всё происходило бы в согласии с принципом автономных превращений энергии ( 4.4). Предельно связанная электрон-позитронная пара не имела бы ничего общего с позитронием, т.е. электрона и позитрона, обращающихся около их общего центра масс – перед тем как проаннигилировать. Позитроний нестабилен, предельно же связанная пара должна быть стабильна. Имея массу электрона и нулевой электрический заряд, она вела бы скрытный образ жизни, не имея возможности входить в какие-либо структуры – и тогда неудивительно, что экспериментаторы могли не заметить её существование в природе. Впрочем, если предельно связанная пара приобрела бы энергию возбуждения 511 кэВ, то произошла бы диссоциация её на составляющие – что выглядело бы как рождение электрон-позитронной пары!

Как можно видеть, наш подход объясняет происхождение характеристического значения энергии гамма-квантов анигиляции – но на один акт аннигиляции должен приходиться один такой квант. Традиционный же подход, согласно которому электрон и позитрон при аннигиляции исчезают полностью, предсказывает появление двух характеристических квантов на один акт аннигиляции. Один или два характеристических кванта на один акт аннигиляции – что говорят эксперименты на этот счёт?

Видите ли, эксперименты как раз и ставились в расчёте на то, что при аннигиляции электрон и позитрон исчезают полностью, порождая два кванта по 511 кэВ. И что, по закону сохранения импульса – ведь ортодоксы полагают, что фотоны переносят импульс! – эти два кванта должны разлетаться в противоположных направлениях. И поэтому свидетельствами об актах аннигиляции служили одновременные срабатывания двух детекторов гамма-квантов, расположенных с противоположных сторон от области аннигиляции. Да, одновременные срабатывания детекторов – с точностью до временного разрешения схемы совпадений – имели место. Но имелись ли доказательства того, что детекторы срабатывали на пару квантов, появившихся при одном и том же акте аннигиляции?

Пионерской здесь считается статья Клемперера [К6], которая труднодоступна. К счастью, в статье [Б4] недвусмысленно сказано, что Клемперер « детектировал совпадающие импульсы с двух счётчиков Гейгера, расположенных вплотную к источнику излучения аннигиляции, так что телесный угол, в котором собирал излучение каждый из этих счётчиков, составлял почти 2 » (перевод наш). Конечно, не могло быть гарантий, что совпадения не порождались квантами от независимых актов аннигиляции, случайно совпадавших во времени. Поэтому в дальнейшем исследователи старались улучшить угловое разрешение установки.

Бэринджер и Монтгомери [Б4] в качестве источника излучения аннигиляции использовали активированные кусочки фольги Cu 64, спрессованные в маленькую «пилюлю», которая покрывалась тонким слоем свинца, не пропускавшим наружу позитроны. Такая «пилюля» излучала, практически, в полный телесный угол. Два счётчика располагались на равных расстояниях по разные стороны от неё – с возможностью механической отстройки от «правильной» геометрии, при которой источник и оба счётчика находились на одной прямой. Полученная скорость счёта совпадений, как функция угла отстройки от «правильной» геометрии, вызывает недоумение; мы воспроизводим диаграмму из [Б4] на Рис.4.8 .

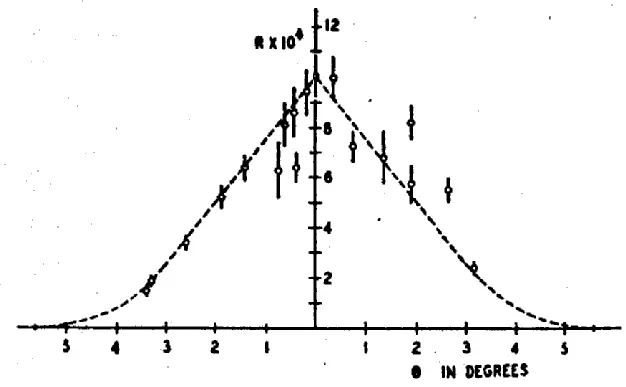
Рис.4.8

Сразу бросается в глаза, что уменьшение скорости счёта совпадений при увеличении угла отстройки выглядит неубедительно: подавляющее большинство точек даёт примерно одну и ту же скорость счёта. Более того: четыре точки, которые дают уменьшенную скорость счёта совпадений при больших углах отстройки, имеют, по сравнению с остальными точками, существенно меньшие доверительные интервалы. А поскольку эти интервалы « вычислены на основе количества отсчётов, взятых в обработку для каждой точки » (перевод наш), то неизбежен вывод: четыре названные точки были получены в иных условиях опыта, чем остальные, а именно – при существенно увеличенных выборках. Нетрудно видеть, к чему это должно было привести. У случайной последовательности импульсов интервалы между двумя соседними импульсами имеют гауссово распределение вероятностей с центром, соответствующим средней частоте появления импульсов. Увеличение выборки не сдвигает центр этого распределения, но изменяет его форму, увеличивая вероятности для значений интервалов в области центра распределения. Соответственно, при этом уменьшаются вероятности для значений интервалов на «крыльях» распределения – в том числе и для коротких интервалов, меньших временного разрешения схемы совпадений. В итоге, увеличение выборки в рассматриваемом эксперименте должно было привести к уменьшению вероятности срабатывания схемы совпадений – и, значит, именно к уменьшению средней скорости счёта совпадений.