Путём включения в схему двоичного суммирующего счётчика (рисунок 60), дополнительных ЛЭ, переключающих на вход последующего триггера прямого и инверсного выходов предыдущего, получается схема реверсивного счётчика. Фрагмент схемы реверсивного счётчика приведён на рисунке 61.
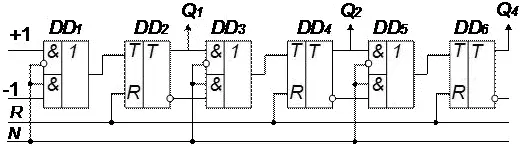
Рисунок 61 Фрагмент схемы реверсивного счётчика
Схема имеет два входа для подачи входных сигналов: +1 — при работе в режиме суммирования, -1 — при работе в режиме вычитания. Дополнительный управляющий вход N задаёт направление счёта. При N=0 схема (рисунок 61) работает как суммирующий счётчик, а при N=1 — как вычитающий.
5.3.4 Счётчики с произвольным коэффициентом счёта
В двоичных счётчиках коэффициент счёта K СЧ =2 nи может быть равен 2, 4, 8, 16, 32 и т.д. На практике требуются счётчики с коэффициентом счёта не равным 2 n, например, 3, 6, 10, 12, 24 и др.
Они выполняются на основе двоичных счётчиков путём исключения у счётчиков с K СЧ =2 nсоответствующего числа «избыточных» состояний S:
S = 2 n– K СЧ
Например, двоично-десятичный (декадный) счётчик получают из 4-х разрядного, имеющего K СЧ =16, исключая 6 состояний.
Возможны 2 варианта построения схем:
а) Счёт циклически идёт от 0000 до 1001, а следующим импульсом обнуляется;
б) Исходным состоянием служит код 0110 числа 6 и счёт происходит до 1111 2=15, а следующим импульсом обнуляется.
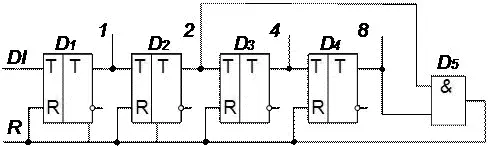
Рисунок 62 Схема счётчика с Ксч =10
Схема счётчика с K СЧ =10, реализованная по первому варианту, приведена на рисунке 62. По сравнению со схемой двоичного счётчика (Рисунок 60), имеющего K СЧ =24=16, в схему дополнительно введён элемент D5, обнуляющий счётчик при совпадении двух «1» с весовыми коэффициентами 2 и 8. Использование приведённой выше схемы и ЛЭ D5 с 4-мя входами, позволит получить счётчик с любым коэффициентом счёта от 2-х до 15-и.
Для реализации схемы по второму варианту используются триггеры, имеющие входы асинхронной установки триггера 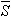 .
.
5.3.5 Счётчики с последовательно-параллельным переносом
Все рассмотренные выше схемы счётчиков представляют собой счётчики с последовательным переносом . В этих счётчиках импульсы, подлежащие счёту, поступают на вход только одного первого триггера, а сигнал переноса передаётся последовательно от одного разряда к другому. Такие счётчики отличаются простотой схемы, но имеют невысокое быстродействие.
Счётчики с параллельным переносом строятся на синхронных триггерах.
Счётные импульсы подаются одновременно на тактовые входы всех триггеров, а каждый из триггеров цепочки служит по отношению к последующим только источником сигналов. Срабатывание триггеров параллельного счётчика происходит синхронно, и задержка переключения всего счётчика равна задержке для одного триггера. Следовательно, такие счётчики более быстродействующие. Их основным недостатком является большая мощность, потребляемая от источника входных сигналов, так как входные импульсы подаются на тактовые входы всех триггеров.
Для устранения недостатков рассмотренных выше счётчиков разработаны и используются счётчики с последовательно-параллельным переносом.
В счётчиках с последовательно-параллельным переносом триггеры объединены в группы так, что отдельные группы образуют счётчики с параллельным переносом, а группы соединяются с последовательным переносом. В роли групп могут быть и готовые счётчики.
Общий коэффициент счёта таких счётчиков равен произведению коэффициентов счёта всех групп.
В качестве примера рассмотрим счётную декаду на JK-триггерах, приведённую на рисунке 63.
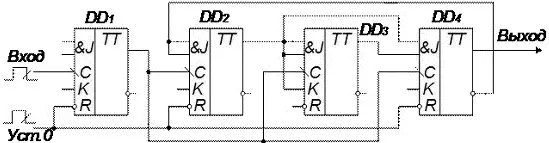
Рисунок 63 Счётная декада на JK-триггерах
Схема состоит из двух групп. Первая группа — это триггер DD1.
Вторая группа, состоящая из трёх триггеров DD2–DD4, представляет собой счётчик с параллельным переносом и тактируется выходным сигналом первого триггера. Группы соединены между собой последовательно.
Схема работает следующим образом.
При подаче на вход импульсов с 1-го по 8-ой декада работает как обычный двоичный счётчик импульсов.
Читать дальше



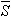 .
.







![Стивен Хокинг - Черные дыры. Лекции BBC [litres]](/books/402420/stiven-hoking-chernye-dyry-lekcii-bbc-litres-thumb.webp)