1.2 Логические основы ЭВМ
Раздел математической логики, изучающий связи между логическими переменными, имеющими только два значения, называется алгеброй логики. Алгебра логики разработана английским математиком Дж. Булем и часто называется булевой алгеброй. Алгебра логики является теоретической базой для построения систем цифровой обработки информации. Вначале на основе законов алгебры логики разрабатывается логическое уравнение устройства, которое позволяет соединить логические элементы таким образом, чтобы схема выполняла заданную логическую функцию.
Таблица 1 – Коды чисел от 0 до 15
| Десятичное число |
Коды |
| Двоичный |
16-ричный |
Двоично-десятичный |
| 0 |
0000 |
0 |
000 |
| 1 |
0001 |
1 |
0001 |
| 2 |
0010 |
2 |
0010 |
| 3 |
0011 |
3 |
0011 |
| 4 |
0100 |
4 |
0100 |
| 5 |
0101 |
5 |
0101 |
| 6 |
0110 |
6 |
0110 |
| 7 |
0111 |
7 |
0111 |
| 8 |
1000 |
8 |
1000 |
| 9 |
1001 |
9 |
1001 |
| 10 |
1010 |
A |
00010000 |
| 11 |
1011 |
B |
00010001 |
| 12 |
1100 |
C |
00010010 |
| 13 |
1101 |
D |
00010011 |
| 14 |
1110 |
E |
00010100 |
| 15 |
1111 |
F |
00010101 |
1.2.1 Основные положения алгебры логики
Различные логические переменные могут быть связаны функциональными зависимостями. Функциональные зависимости между логическими переменными могут быть описаны логическими формулами или таблицами истинности.
В общем виде логическая формула функции двух переменных записывается в виде: y = f ( X 1, X 2), где X 1, X 2— входные переменные.
В таблице истинности отображаются все возможные сочетания (комбинации) входных переменных и соответствующие им значения функции y, получающиеся в результате выполнения какой-либо логической операции. При одной переменной полный набор состоит из четырёх функций, которые приведены в таблице 2.
Таблица 2 – Полный набор функций одной переменной
| X |
Y1 |
Y2 |
Y3 |
Y4 |
| 0 |
1 |
0 |
1 |
0 |
| 1 |
0 |
1 |
1 |
0 |
Y1 — Инверсия, Y2 — Тождественная функция, Y3 — Абсолютно истинная функция и Y4 – Абсолютно ложная функция.
Инверсия (отрицание) является одной из основных логических функций, используемых в устройствах цифровой обработки информации.
При двух переменных полный набор состоит из 16 функций, однако в цифровых устройствах используются далеко не все.
Основными логическими функциями двух переменных, используемыми в устройствах цифровой обработки информации являются: дизъюнкция (логическое сложение), конъюнкция (логическое умножение), сумма по модулю 2 (неравнозначность), стрелка Пирса и штрих Шеффера. Условные обозначения логических операций, реализующих указанные выше логические функции одной и двух переменных, приведены в таблице 3.
Таблица 3 Названия и обозначения логических операций

Операцию инверсии можно выполнить чисто арифметически: 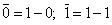 и алгебраически:
и алгебраически: 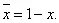 Из этих выражений следует, что инверсия x , т.е.
Из этих выражений следует, что инверсия x , т.е. 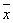 дополняет x до 1. Отсюда и возникло ещё одно название этой операции — дополнение . Отсюда же можно сделать вывод, что двойная инверсия приводит к исходному аргументу, т.е.
дополняет x до 1. Отсюда и возникло ещё одно название этой операции — дополнение . Отсюда же можно сделать вывод, что двойная инверсия приводит к исходному аргументу, т.е. 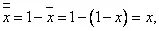 и это называется законом двойного отрицания.
и это называется законом двойного отрицания.
Таблица 4 – Таблицы истинности основных функций двух переменных
| Дизъюнкция |
Конъюнкция |
Исключающее ИЛИ |
Стрелка Пирса |
Штрих Шеффера |
| X1 |
X2 |
Y |
X1 |
X2 |
Y |
X1 |
X2 |
Y |
X1 |
X2 |
Y |
X1 |
X2 |
Y |
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
| 0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
| 1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
Дизъюнкция. В отличие от обычного арифметического или алгебраического суммирования здесь наличие двух единиц даёт в результате единицу. Поэтому при обозначении логического суммирования предпочтение следует отдать знаку (∨) вместо знака (+) [1].
Читать дальше


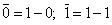 и алгебраически:
и алгебраически: 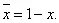 Из этих выражений следует, что инверсия x , т.е.
Из этих выражений следует, что инверсия x , т.е. 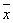 дополняет x до 1. Отсюда и возникло ещё одно название этой операции — дополнение . Отсюда же можно сделать вывод, что двойная инверсия приводит к исходному аргументу, т.е.
дополняет x до 1. Отсюда и возникло ещё одно название этой операции — дополнение . Отсюда же можно сделать вывод, что двойная инверсия приводит к исходному аргументу, т.е. 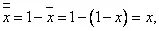 и это называется законом двойного отрицания.
и это называется законом двойного отрицания.






![Стивен Хокинг - Черные дыры. Лекции BBC [litres]](/books/402420/stiven-hoking-chernye-dyry-lekcii-bbc-litres-thumb.webp)