Джордж Массер - Нелокальность - Феномен, меняющий представление о пространстве и времени, и его значение для черных дыр, Большого взрыва и теорий всего

Энергия достигает максимума в полностью взаимосвязанной сети, где каждая крупинка соединена со всеми остальными. В такой сети принцип локальности не соблюдается — вы можете перейти от отдельно взятой крупинки к любой другой крупинке одним скачком без прохождения через промежуточные точки. В сети отсутствует иерархия связей — близкое-далекое, маленькое-большое, — которая характерна для пространства. Вы не можете разделить ее на отдельные части — это неделимое целое. «В этой сущности нет понятия локальности… — объясняет Маркопоулоу. — Если вы просто протянете руку, то сможете дотянуться до всего в целой Вселенной».

Чтобы понять, почему высокоэнергетическая сеть непространственна, попытайтесь присвоить местоположение крупинкам. Каждая из них должна быть равноудаленной (один прыжок) от любой другой. Для первых трех крупинок это не проблема — расположите их в вершинах равностороннего треугольника. Четыре крупинки можно расположить в виде пирамиды. Но что делать с пятой? Местоположения, равноудаленного от первых четырех крупинок, не существует, по крайней мере в обычном трехмерном пространстве. Вам необходима четырехмерная пирамида. На деле каждая следующая крупинка требует нового измерения пространства. Очень быстро вы получите ультрамногомерный мир, который невозможно визуализировать. И по большей части это гигантское нагромождение не нужно — сеть имеет ширину всего в один прыжок в любом направлении и очень сильно похожа на скатанную в шар паутину. Поэтому, хотя можно по-прежнему рассуждать о сети как о существующей в пространстве, это не то пространство, которое нам нужно: три измерения, тянущиеся настолько, насколько мы можем видеть, в каждом направлении и позволяющие удобно описывать взаимосвязи между объектами.

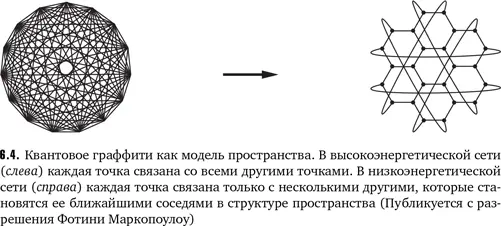
Низкоэнергетические модели — это отдельная история. Это то, что нам нужно. Каждая крупинка соединяется всего лишь с несколькими другими, образуя правильную решетку вроде сот или ткани. Понятие расстояния обретает смысл: одни крупинки находятся ближе друг к другу, другие дальше. Сеть прекрасна и просторна. Принцип локальности соблюдается: чтобы воздействие передалось из одного места в другое, оно должно не перепрыгнуть, а проделать определенный путь по сети. На прохождение сигнала требуется время, которое объясняет, почему скорость объектов в пространстве ограничена (скоростью света).

Короче говоря, отсутствие и наличие пространства — это просто два разных фазовых состояния одной и той же сети крупинок. Одно может переходить в другое — скомканная масса может распрямляться и становиться плоской. Теоретики уже предложили парочку путей, которыми может идти этот процесс. Изменение формы может происходить во времени. Сеть возникает как нечто раскаленное — высоко взаимосвязанная модель содержит огромное количество энергии. Затем она остывает и кристаллизуется, подобно превращению воды в тарелке в лед, по мере разрушения связей и приобретения формы аккуратной структуры. Хитрость заключается в объяснении остывания. Объекты не остывают сами по себе, что-то должно уносить из них тепло. «Куда уходит энергия? — спрашивает себя Маркопоулоу. — Нужен какой-то холодильник. Вселенную нужно охлаждать». Она с коллегами предполагает, что энергия может уходить на создание материи. Первоначальные крупинки могут агрегироваться и образовывать элементарные частицы, поэтому материя появляется одновременно с пространством.

Как вариант переход может не быть процессом, развивающимся во времени, а структурой, которая возникает на квантовом уровне. Сеть способна существовать сразу во многих состояниях, в переходной стадии, известной как суперпозиция. Хотя большинство этих состояний непространственные, они могут сливаться во что-то пространственное. Наиболее проработанное представление о суперпозиции пространства носит довольно громоздкое название «каузальная динамическая триангуляция». Ее изобретатели показали, что непространственные геометрии нейтрализуют друг друга, поскольку события высокоорганизованны и различие между причиной и следствием появляется с самого начала. Этот эффект подобен коллективному разуму, тем замечательным ситуациям, когда вы задаете вопрос группе, в которой ни у кого нет правильного ответа, но объединение всех предположений позволяет найти его. Классический пример — эксперимент с конфетами: если спросить группу людей, сколько конфет в вазе, то усредненный ответ будет лучше любого отдельно взятого ответа. Коллективный разум группы превосходит разум ее членов.