Pичард Фейнман - Характер Физических Законов

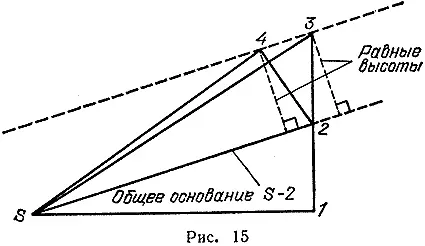
Это означает, что тело двигалось по линии 1-2 и продолжало бы двигаться по ней, если бы не было силы, но притяжение Солнца заставляет тело двигаться по линии 2-S. Таким образом, движение тела на следующем отрезке складывается из того, как планета двигалась бы самостоятельно, и изменения, которое произошло под действием Солнца. Поэтому планета попадает не в положение 3, а в положение 4.

Теперь мы сравним площади треугольников 23S и 24S и докажем, что они равны. У них общее основание S-2. Одинаковы ли у них высоты? Да, потому что треугольники заключены между параллельными линиями. Расстояние от точки 4 до линии 5-2 равно расстоянию от точки 3 до линии 5-2 (продолженной). Значит, площадь у треугольника S24 такая же, как у S23. Раньше я доказал, что треугольники S12 и S23 равны по площади. Отсюда ясно, что S12=S24. Таким образом, при движении планеты по орбите площади, описываемые за первую и за вторую секунду, равны. Значит, путем рассуждений мы нашли связь между тем фактом, что сила направлена к Солнцу, и тем фактом, что площади равны. Не правда ли, остроумно? Я позаимствовал вывод прямо у Ньютона. Все это содержится в его "Principia": и схема, и доказательство. Только цифры другие, потому что он пользовался римскими цифрами, а я - арабскими.

Все доказательства в книге Ньютона были геометрическими. Сегодня мы строим доказательства по-другому. Мы доказываем аналитически, при помощи символов. Чтобы построить нужные треугольники, подметить равенство площадей, требуется изобретательность. Теперь мы имеем усовершенствованные методы анализа, более быстрые и эффективные. Я хочу показать вам, как это выглядит в обозначениях более современной математики, где для доказательства нужно лишь записать несколько символов.

Мы будем говорить о быстроте изменения площади и обозначим эту величину через А'. При повороте радиуса площадь изменяется, и быстрота ее изменения - это составляющая скорости, перпендикулярная радиусу, умноженная на радиус. Иначе говоря, это расстояние по радиусу, умноженное на скорость, т. е. на быстроту изменения расстояния:

A = r x r'

Спросим себя: изменяется ли сама скорость изменения площади? Закон Кеплера говорит, что скорость изменения площади не должна меняться. Поэтому мы дифференцируем написанное равенство, а тут весь фокус в том, чтобы поставить точки в нужных местах - и ничего больше. Таким фокусам надо научиться: это просто набор правил, которые были придуманы, чтобы облегчить доказательства. Мы пишем

A'' = r' x r' + r x r'' = r x F/m.

Первое слагаемое - это составляющая скорости, перпендикулярная самой скорости. Оно равно нулю - скорость направлена вдоль самой себя. Ускорение r''- это вторая производная r, т.е. производная скорости. Она равна силе, деленной на массу.

Это означает, что скорость изменения скорости изменения площади есть составляющая силы, направленная под прямым углом к радиусу. Но если сила направлена по радиусу,

r x F / m = 0

как утверждал Ньютон, то под прямым углом к радиусу она не действует, а значит, скорость изменения площади не изменяется:

A'' = 0.

Мы видим, как много нам дает анализ при помощи символов. Ньютон более или менее умел это делать, только в несколько других обозначениях. Но он предпочел геометрические доказательства, стремясь к тому, чтобы люди могли прочесть его статьи. Он сам изобрел исчисление бесконечно малых, которым я воспользовался во втором доказательстве.

Это хорошая иллюстрация взаимоотношений между математикой и физикой. Когда в физике проблема оказывается трудной, мы можем заглянуть к математикам - вдруг они уже встречались с такими вопросами и имеют готовые способы доказательства? Но может оказаться, что они этим еще не занимались. Тогда нам придется самим изобрести доказательства и потом передать их математикам.

Каждый кто рассуждает о чем-нибудь точно, показывает тем самым, как человек мыслит, и если представить его рассуждения в общем виде и передать математикам, то они внесут его в свои книги в качестве раздела математики. Математика - это путь, по которому мы переходим от одной совокупности утверждений к другой. И она, очевидно, полезна в физике, потому что говорить о вещах мы можем по-разному, а математика позволяет нам выяснить следствия, анализировать ситуации и видоизменять законы, чтобы связать различные утверждения. В общем физик знает очень мало. Он только должен помнить правила, которые позволяют переходить от одного к другому, ибо все эти различные утверждения о равенстве интервалов времени, о силе, направленной по радиусу, и т.д. тесно связаны логикой.