Питер Эткинз - Десять великих идей науки. Как устроен наш мир.

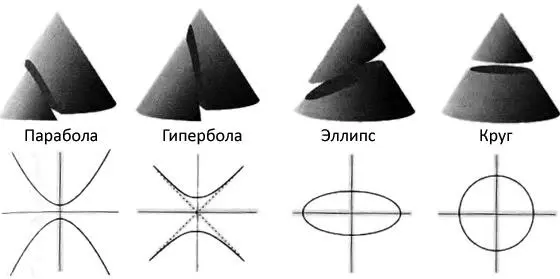
Рис. 10.4.У греков было абстрактное представление о пространстве, и поэтому они преуспели в геометрии. Здесь мы видим, как параболы, гиперболы и эллипсы (включая частный случай круга) можно рассматривать как наборы чисел, получаемые посредством сечений конуса в разных направлениях. Теперь мы знаем, благодаря пионерской работе Декарта, как связать эти формы с алгебраическими уравнениями, и поэтому можем видеть связи между геометрией пространства и арифметическими свойствами определенных наборов чисел.

На самом деле, арифметика даже более богата. В соответствии с чрезвычайно важной, но обманчиво краткой теоремой, которую доказал в 1915 г. немецкий математик Леопольд Лёвенгейм (1878-1957) и усовершенствовал в 1920 г. норвежец Альберт Тораф Сколем (1887-1963), система правил, подобных правилам арифметики, действует в любой области знания, которая может быть формализована в терминах набора аксиом. Если бы в школе вам говорили, что, согласно теореме Лёвенгейма-Сколема , вы, на самом деле, моделируете процесс вывода заключений из квантовой механики, теории естественного отбора и юриспруденции (постольку, поскольку эти области знания могут быть выражены в терминах аксиом), это могло бы смягчить утомление от узнавания, как извлекать квадратный корень и проделывать длинные упражнения на деление. То же самое верно относительно остальной части этой главы: хотя многое в ней будет читаться, как относящееся к арифметике, имейте в виду, что это в действительности относится к любой систематизированной области человеческого знания . Если уж это не захватывает дух, то я просто не знаю, чем вас пронять.

Некоторые иррациональные числа, включая π , но не √2, являются трансцендентными, в том смысле, что они «трансцендируют», переступают обычные алгебраические уравнения. Это просто означает, что они не являются решениями простых алгебраических уравнений, подобных 3x 2− 5x + 7 = 0 . Так, x = √2 есть решение уравнения х 2− 2 = 0 , поэтому (как решение такого уравнения), это число алгебраическое, а не трансцендентное. Однако не существует уравнения такого вида, решением которого было бы x = π или x = e , поэтому π и e не только иррациональные, но и трансцендентные числа. В 1934 г. русский математик Александр Гельфонд (1906-68) доказал, что a b является трансцендентным, если a алгебраическое (отличное от 0 и 1) число, a b — алгебраическое и иррациональное (как √2); так, 2 √2, например, трансцендентно, поскольку 2 — алгебраическое, а иррациональное число √2 — тоже алгебраическое. Поэтому мы сразу знаем, что не существует алгебраического уравнения, решением которого было бы 2 √2. Между прочим, название «алгебра», которое только что появилось, произошло от Al-jabr w'al muqâbala (Восстановление и упрощение), названия книги Мухаммеда ибн Муса аль-Хорезми, написанной в 830 г. Al-jabr , «возвращение», здесь относится к решению уравнений, но очаровательно, что этот термин означает также и «костоправ». Аль-Хорезми отличился дважды: его имя тоже является источником термина «алгоритм», обозначающего серию процедур для решения уравнений.

Мы видели, что решения различных уравнений порождают классы чисел, известные под общим названием «алгебраические числа». Решения уравнений, подобных 2x = 1 , дают нам рациональные числа (в данном случае x = 1/2), в то время как уравнения, подобные x 2= 2 , дают нам иррациональные числа (в данном случае x = √2); числа, не являющиеся решениями уравнений, подобных этим, являются трансцендентными числами (как x = 2 √2). Натуральные числа можно представить как решения уравнений, подобных x − 2 = 1 (с решением x = 3), а отрицательные числа как решения уравнений, подобных x + 2 = 1 (с решением x = − 1). Но существует простое уравнение, выпадающее из этого списка: каково решение уравнения x 2+ 1 = 0 ? Ни одно из чисел введенных ранее не является его решением, поскольку квадрат любого из них положителен и, будучи прибавлен к 1, не может дать нуля. В значительной мере потому, что математики не хотели признавать, что некоторые уравнения не имеют решения, они ввели понятие мнимого числа i , которое является решением уравнения x 2+ 1 = 0 ; другими словами, x = √( − 1). Поскольку они — на самом деле, Декарт — считали, что чисел, подобных i и i , умноженному на любое число, в действительности не существует, они и назвали их «мнимыми».