Артур Уиггинс - Пять нерешенных проблем науки

В дальнейшем, если развитые страны уменьшат потребление ископаемого топлива и обратятся к возобновляемым источникам энергии типа водяных, ветряных и солнечных, остроту проблемы потепления удастся снять. В Европе используют ядерную энергию, но ее производство и потребление сопряжено с вопросами безопасности и утилизации отходов. Далее, странам третьего мира необходимо снизить уровень рождаемости. Прежде чем проводить в жизнь тот или иной план, следует учесть все этические, экономические и политические факторы.

В ходе формирования Земли тяготение сортировало первичный материал в соответствии с его плотностью: более плотные составляющие опускались к центру, а менее плотные плавали сверху, образовав в итоге кору. На рис. I.8 представлена Земля в разрезе.

Она обладает наименьшей плотностью и расколота на многочисленные тонкие и жесткие каменные плиты, медленно движущиеся ввиду перемещения нижележащей мантии.

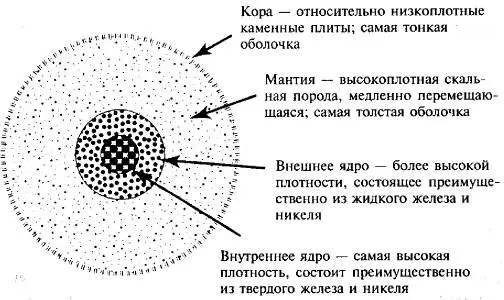
Рис. I.8. Строение Земли

Она самая толстая из всех оболочек, относительно теплая и жидкая по сравнению с корой, имеет горячие точки, порождающие конвекционные потоки (представьте завихрения в закипающей воде, только значительно медленнее движущиеся). Потоки в мантии перемещают плиты, вызывая землетрясения, вулканические извержения, расширение морского дна и дрейф континентов.

Далее идет горячее жидкое внешнее ядро, состоящее из плотного железа и никеля и плещущееся ввиду вращения Земли. Земной магнетизм, возможно, вызван местным движением внутри этой оболочки.

Самая нижняя оболочка именуется внутренним ядром. Она хотя и состоит из расплавленного железа и никеля, из-за огромного давления оказывается твердой и самой плотной оболочкой.

За подробностями процесса создания этой модели и подтверждающими ее опытными данными обращайтесь к нашей книге Пять крупнейших представлений в науке (The Five Biggest Ideas in Science. N.Y.: John Wiley and Sons, Inc., 1997).

Следующие узлы Всемирной Паутины содержат свежую информацию и прекрасные иллюстративные материалы:

www. hartrao. ас. za/geodesy/tectonics.html

http://pubs.usgs.gov/peubications/text/dynamic.html

www.seismo.unr.edu/ftp/pub/louie/class/100/plate-1ectonics.html

http://scign.jpl.nasa.gov/lwarn/plate/htm

Как уже говорилось в гл. 5, хаос не следует путать с произволом. Хаос означает скорее чрезвычайную восприимчивость конечного результата к малым изменениям в начальных условиях. Как поется в старой колыбельной:

До 1960-х годов существовал некий сугубо математический метод, как оказалось, связанный с теорией хаоса. Гастон Морис Жулиа, математик из Алжира, после ранения в сражениях Первой мировой войны вынужден был носить на лице кожаную повязку, защищавшую сильно искалеченный нос. Из-за многочисленных операций ему приходилось долго скитаться по госпиталям, где, чтобы как-то скоротать время, он занимался математическими выкладками. В 25 лет он пишет «Записку о приближении рациональных функций». Работу он делал в связи с темой, объявленной в 1915 году Французской академией наук на соискание главной премии 1918 года, которой и удостоился; хотя французский математик и астроном Пьер Жозеф Луи Фату (1878–1929) опубликовал в декабре 1917 года работу на ту же тему, однако Жулиа отослал свою статью в Академию наук раньше. Функция представляет собой математическое правило вычисления наподобие следующего: f(x) — х 2+ const. Если x = 2, а const = 3, то значение функции составит 7. Приближение (итерация) осуществляется использованием вычисленного для f значения в качестве следующего значения для х. Итак, если х = 7, то f (х) = 52, и т. д. Жулиа исследовал более сложные выражения. Особо его занимали функции и значения, при которых возможно многократное приближение без бесконечного роста итоговой величины [самой функции]. Значения х, для которых повторяющиеся итерации давали конечный результат, стали именоваться пленниками [обычно говорят о множестве точек притяжения, или аттракторах]. При стремлении к бесконечности итоговых величин их называют «беглецами» [обычно говорят о множестве точек отталкивания, или репеллерах]. Вычисления велись вручную и были крайне трудоемкими даже для простых функций. Хотя Жулиа и обрел некую славу в математических кругах, его труд был основательно забыт, и вспомнили о нем уже в 1970-е годы.