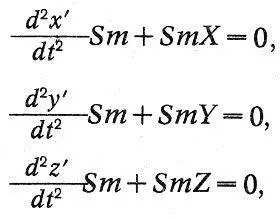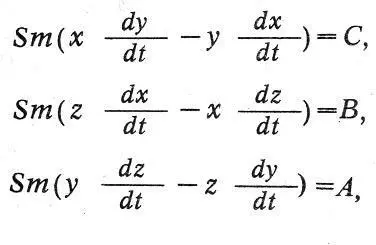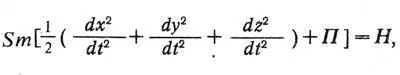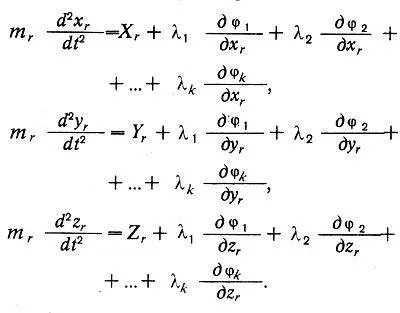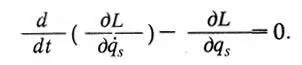Кудрявцев Степанович - Курс истории физики

где S - знак суммы; m - масса каждого из тел (точек) системы; х, у, z - координаты тела (точки); Р, Q, R, ...— заданные ускоряющие силы, действующие на единицу массы по направлению соответствующих центров; р, q, r,... — расстояния тел (точек) от этих центров; δр, δq, δr, ... — вариации этих расстояний.

Из этой общей формулы Лагранж выводит законы и уравнения движения системы. Закон движения центра тяжести он формулирует так: «Движение центра тяжести системы свободных тел, расположенных одно по отношению к другому совершенно произвольным образом, всегда таково, как если бы все тела были сосредоточены в одной точке и если бы в то же время каждое из них находилось под действием тех же ускоряющих сил, под влиянием которых оно находится в своем действительном состоянии». Аналитически эта теорема записывается Лагранжем в следующем виде:

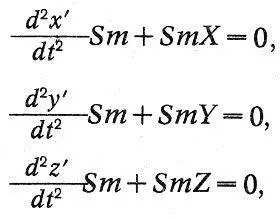
где x', y', z' — координаты центра тяжести.

Теорему площадей для центральных сил Лагранж записывает в следующем виде:

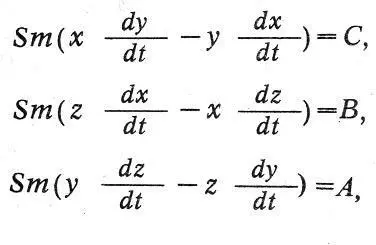
где А, В, С — произвольные постоянные. Принцип сохранения живых сил Лагранж выражает в виде:

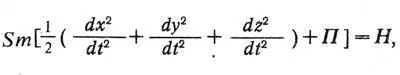
где H обозначает произвольную постоянную, равную значению левой части уравнения в заданное мгновение; П — функция, дифференциал которой равен:

dП = Pdp + Qdq + Rdr+...,

т. е., по современным представлениям, равен элементарной работе движущих сил; однако Лагранж термина «работа» не знал, равно как и термина «энергия ». Написанную выше формулу, выражающую закон сохранения энергии для консервативных сил, Лагранж называет принципом сохранения живых сил.

Далее Лагранж выводит дифференциальные уравнения движения системы. Мы их выпишем в более привычной форме. Если уравнения связей системы: φ 1 = О, φ 2 = О, ...φк = 0, то уравнения Лагранжа первого рода имеют вид:

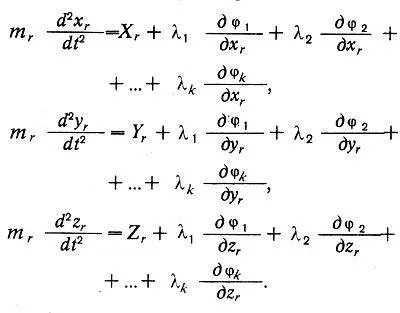
Лагранж делает следующий важный шаг: он вводит новые переменные, «пользование которыми может максимально облегчить интегрирование». Эти «обобщенные координаты» соответствуют числу «степеней свободы», т. е. числу тех независимых параметров, которые полностью характеризуют систему. Применяя метод наименьшего действия, Л агранж получает уравнения:

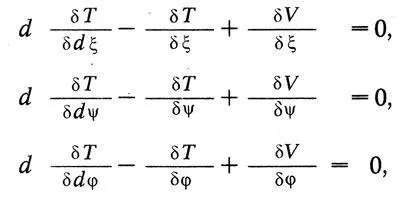
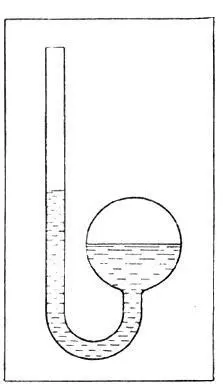
Рис. 23. Воздушный термометр Амонтона

Число уравнений «в точности равно числу переменных, Ф, ..., от которых зависит положение системы в каждое мгновение». Сейчас обобщенные координаты обозначают символом, потенциальную энергию — символом U, сохраняя для кинетической энергии обозначение Лагранжа Т. Тогда, введя функцию Т - U, которую в честь Лагранжа обозначают L, его уравнения записывают так:

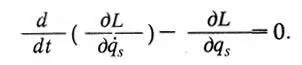
В современной теоретической физике уравнения Лагранжа приобрели огромное значение, далеко выходящее за пределы механики. Они применяются в термодинамике, электродинамике, атомной физике. Таким образом, Лагранж создал мощный метод, позволяющий решать большой круг задач.

Ирландский математик, механик и астроном У.Р.Гамильтон, оценивая вклад, внесенный Лагранжем в развитие механики после Галилея и Ньютона, писал: «Из числа последователей этих блестящих ученых Лагранж, пожалуй, больше, чем какой-либо другой аналитик, сделал для того, чтобы расширить и придать стройность подобным дедуктивным исследованиям, доказав, что самые разнообразные следствия, относящиеся к движению системы тел, могут быть выведены из одной основной формулы. При этом красота метода настолько соответствует достоинству результата, что эта великая работа превращается в своего рода математическую поэму». Этой поэмой завершился плодотворный период разработки основ теоретической механики.