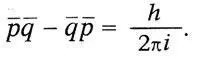Кудрявцев Степанович - Курс истории физики

Паули очень неодобрительно встретил статью Уленбека и Гаудсмита. Еще ранее он отнесся отрицательно к аналогичной идее, высказанной Кронигом.

Бор и Гейзенберг, наоборот, проявили большой интерес к новой гипотезе, а после того как Томас вычислил на основе гипотезы спина значение дублетного расщепления, Паули снял свои возражения.

Таким образом, 1925 г. оказался годом рождения квантовой механики Гейзенберга и Дирака, годом рождения новой квантовой статистики Бозе — Эйнштейна, годом рождения принципа Паули и гипотезы спина.

Вольфганг Паули, один из активных деятелей современной физики, родился в Швейцарии 25 апреля 1900 г.

Он окончил Мюнхенский университет и, еще будучи студентом, написал статью-монографию «Теория относительности», опубликованную в Математической энциклопедии в 1921 г.

Рис. 77. Н. Бор и В. Паули

Успех публикации побудил издать ее отдельной книгой, вышедшей с предисловием А. Зоммерфельда в том же, 1921 г. Русский перевод ее вышел в 1947 г.

По окончании университета Паули работал в Геттингене (1921—1922), Копенгагене (1922—1923), Гамбурге и с 1927 г. в Цюрихе, в Высшем техническом училище (политехникуме). Открытие принципа Паули дало ключ к объяснению периодической системы химических элементов Д. И. Менделеева и вместе с открытием спина послужило основой новой формы квантовой статистики для частиц, обладающих полуцелым спином. Эта статистика была создана Э. ферми, сообщившим о ней в короткой заметке 6 февраля 1926 г. и в статье «О квантовании идеального газа», опубликованной 26 марта 1926 г. Статья Дирака была представлена Лондонскому Королевскому обществу 26 августа того же года. Таким образом, 1926 г. был годом создания статистики ферми — Дирака.

Открытие принципа Паули было удостоено в 1945 г. Нобелевской премии.

В 1931 г. Паули предложил гипотезу новой частицы, названной по предложению ферми «нейтрино».

Умер Паули 16 декабря 1958 г.

Возвратимся к истории создания квантовой механики. В матричной механике Гейзенберга — Борна — Иордана каноническим переменным q и р классической механики соответствовали матрицы q и p. Существенно, что произведение матриц не удовлетворяло закону переместительности, а выполнялось перестановочное соотношение:

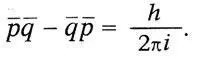
Как мы видели, Дирак обратил особое внимание на это соотношение, тогда как «копенгагенцы» поняли его значение лишь позже, после построения математической схемы квантового излучения.

Оперируя бесконечными матрицами, Гейзенберг, Паули, Борн и Иордан решили ряд задач атомной механики. «Математика, — писал впоследствии Гейзенберг об этом начальном периоде квантовой механики, — неожиданно проявила себя «умнее» физики; и здесь мы опять встречаемся с тем случаем в теоретической физике, когда с помощью такой математики нападают на след новых открытий».

«Позднее,— продолжал Гейзенберг, — Борну, Иордану и Дираку полностью удалось проникнуть во внутреннюю структуру подобного рода математики и успешно применить математическую схему к расчету атома». Гейзенберг особо подчеркивает роль Борна, Иордана, а также Дирака в разработке математической схемы квантовой механики. «В работах Борна и Иордана,— писал он, — матричная механика впервые стала законченной математической схемой».

Вслед за этой математической теорией начала создаваться другая теория атомных процессов, исходящая из совершенно новых основ. В начале 1926 г. в журнале «Annalen der Physik» появились две статьи Шредингера на тему «Квантование как проблема собственных значений» (27 января и 23 февраля 1926г.). 18 марта того же года поступила статья «Об отношении механики Гейзенберга —Борна —Иордана к моей». Третье сообщение из цикла «Квантование как проблема собственных значений» поступило 10 мая 1926 г. четвертое, последнее сообщение того же цикла поступило 21 июня 1926 г В ноябре 1926 г. Шредингер собрал все работы, опубликованные в «Annalen der Physik», прибавил к ним небольшую заметку, опубликованную в «Die Naturwissenschaften», — «Непрерывный переход от микро- к макромеханике» и издал их отдельной книгой, вышедшей в 1927 г. под общим названием «Статьи по волновой механике».

Шредингер исходил из идей де Бройля и оптико-механической аналогии Гамильтона. По этой аналогии геометрической оптике соответствуют уравнения классической механики, определяющие траекторию частицы, так же как законы геометрической оптики определяют форму лучей света. Геометрическая оптика применима к малым длинам волн; когда же длиной волны нельзя пренебречь, то вступают в силу законы волновой оптики, описываемые волновым уравнением.