Яков Гегузин - Живой кристалл

Сделанным замечанием, разумеется, идея Френкеля не порочится, потому что замечание носит характер не принципиальный, а только количественный: потребная флуктуация энергии велика, и поэтому образование «пары» маловероятно.

В те годы, когда френкелевская идея только появилась, ясного понимания ее неприменимости к объяснению опытов Иоффе не было. Конец рассказанной мной истории тогда казался истинно счастливым. Иллюзорность согласия теории и эксперимента выяснилась позже, но большое событие в истории науки произошло, «пары Френкеля» родились, идея дефектов, существование которых предсказывает термодинамика, появилась и прочно вошла в ткань науки о кристаллах, повлияв на развитие многих ее разделов.

Опыты Иоффе количественно были объяснены немного позже. Для этого была использована идея, лишь чуть-чуть отличающаяся от той, из которой следуют «пары». О ней я рассказывать не стану. Здесь мне, однако, хочется высказать почти самоочевидную сентенцию: внутренне непротиворечивая, глубоко физическая идея может оказаться жизнеспособной и значащей и тогда, когда она оказывается бессильной объяснить факты, для объяснения которых была рождена.

В заключение очерка несколько фраз о «втором дыхании идеи». Когда физики и инженеры начали активно заниматься исследованиями последствий взаимодействия ядерных излучений с веществом — это было в конце 40-х — начале 50-х годов, — идея «пары» привлекла их пристальное внимание. Как выяснилось, под влиянием облучения атом может покинуть узел принудительно, не ожидая необходимой для этого энергии, которая ему может быть доставлена волей случая. Атом выбивается из узла и застревает в одном из ближайших междоузлий — образуется «пара».

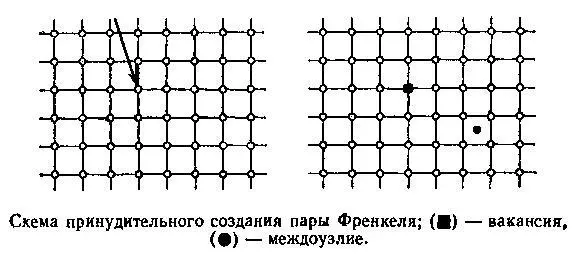
В этом радиационном варианте «пара Френкеля» — один из основных типов дефектов, которые возникают в кристаллах при их облучении протонами, нейтронами, γ-квантами и др. Именно в радиационном варианте «пара Френкеля» обрела второе дыхание.

Идея заморозить пустоту возникла задолго до того, как о ней стали писать в научных журналах и докладывать на научных конференциях.

Ссылки на «частное сообщение» особой доказательностью не отличаются. Но в данном случае иной ссылки быть не может, и, рассказывая о том, как родилась идея «заморозить пустоту», я могу сослаться лишь на «частное сообщение».

Борис Георгиевич Лазарев — крупный специалист в области физики низких температур, один из поколения физиков, начинавших свою деятельность в «школе Иоффе», — мне рассказывал о том, что Яков Ильич Френкель советовал ему «заморозить пустоту» еще в середине 30-х годов, т. е. почти за двадцать лет до того, как Б. Г. Лазарев одним из первых эту идею осуществил.

Речь идет вот о чем. При высокой температуре в кристаллической решетке концентрация вакансий — «атомов пустоты» — велика. Впрочем, лучше выразиться точнее: «велика» — значит всего около сотой процента

позиций в решетке вакантны. Если температуру понижать, то и концентрация вакансий должна понизиться. Важно, с какой скоростью будет происходить понижение температуры и уменьшение концентрации вакансий. Если температуру понижать медленно, вопрос не возникает: концентрация вакансий будет в точности соответствовать равновесной при данной температуре образца.

В принципе мыслимо (видимо, так рассуждал Я. И. Френкель) температуру понижать с такой скоростью, что вакансии, которые при понижении температуры оказываются лишними и которым надлежит как-то уходить из кристаллической решетки, не будут успевать это делать. У вакансий есть много способов исчезнуть, уйти из кристаллической решетки. Не будем их обсуждать, нам вполне достаточно знать, что как-то вакансии могут уйти. А при низких температурах, когда диффузионная подвижность вакансий пренебрежимо мала, они практически вообще этого делать не будут. Это значит, что вакансии, т. е. атомы пустоты, окажутся замороженными. Именно это и имеется в виду, когда говорят «замороженная пустота». Так можно заморозить песчинки в быстро охлаждаемой воде, в которой взмучен песок. Если бы вода остывала медленно, песок успел бы осесть на дно.

Замороженные вакансии должны увеличить омическое сопротивление металлического кристалла на некоторую величину ∆ R. Так как каждая из них является центром, рассеивающим электроны, то