Яков Перельман - Физика на каждом шагу

6 000 000 000 000 000 000 000 тонн.

Если бы мы отвешивали такую массу на весах и каждую секунду клали на чашку миллион тонн, то знаете, сколько времени должны были бы мы безостановочно, день и ночь, работать, чтобы закончить такое отвешивание? Двести миллионов лет! А ведь один миллион тонн во много раз тяжелее самых тяжелых сооружений, возведенных руками человека. Эйфелева башня весит всего 9 000 тонн, а корабли-исполины – линкоры и плавающие пассажирские дворцы – не тяжелее 30–50 тысяч тонн.

Тем удивительнее должна нам казаться научная изобретательность человека, который сумел измерить этот чудовищный груз, сумел взвесить ту планету, на которой он живет.

Конечно, в действительности опыт был обставлен не так просто, как мы изобразили. Чтобы сделать его суть понятнее, нам пришлось упростить его, отбросив все подробности. Притяжение свинцового шара настолько слабо, что для его обнаружения и измерения потребовался целый набор очень точных и сложных инструментов, устройство которых представляет интерес только для тех, кто намерен и имеет возможность сам повторить этот опыт.

Прыжок с места на высоту одного метра считался в легкой атлетике довольно хорошим достижением, а прыжок на высоту полутора метров являлся уже рекордным [3]. Но как следует при этом мерить высоту прыжка?

Казалось бы, естественнее всего определять, на какое наибольшее расстояние удаляется от земли нижняя точка тела. Если так оценивать величину прыжка вверх, то из трех прыжков, изображенных на рис. 9, самый высокий – прыжок через барьер (крайняя правая фигура). Ведь это подъем на высоту чуть не полутора метров, между тем как на второй фигуре мы видим прыжок всего на высоту каких-нибудь 30–40 см.

Может быть, иной физкультурник так и расценит эти прыжки. Но если вы предложите оценить их физику, он удивит вас заявлением, что все три прыжка одинаковы по затраченной мускульной энергии. Почему? Потому что во всех случаях центр тяжести тела поднят на одну и ту же высоту. Центр тяжести человеческого тела находится там, где поставлено черное пятнышко на нашем рисунке. И вы видите, что три пятнышка прыгающих фигур находятся на одном и том же уровне, несмотря на различное положение тела прыгунов. А затрачиваемая энергия зависит только от того, как высоко поднят центр тяжести тела.

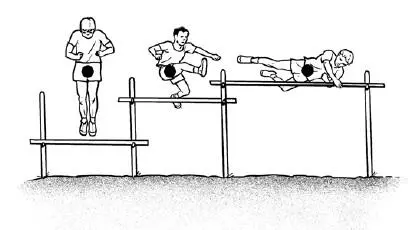
Рис. 9. Прыжки через барьер. Черное пятнышко на фигурах обозначает центр тяжести человеческого тела

Сталкиваются ли между собою две лодки, два трамвайных вагона, два крокетных или биллиардных шара, несчастный ли это случай или только очередной ход в игре, – физик обозначает такое происшествие одним коротким словом: удар. Удар длится миг, но если ударяющиеся предметы, как обычно и бывает, упруги, то в это краткое мгновение успевает совершиться весьма многое. В начале удара оба столкнувшихся предмета сжимают друг друга в том месте, где они соприкасаются. Наступает момент, когда взаимное сжатие достигает наибольшей степени; внутреннее противодействие, возникшее в ответ на сжатие, мешает дальнейшему сжатию, уравновешивая надавливающую силу. В следующий момент сила противодействия, стремясь восстановить форму тела, расталкивает предметы в противоположные стороны: ударяющий предмет получает свой удар обратно. И мы действительно наблюдаем, что если, например, биллиардный шар ударяет в другой такого же веса, но неподвижный, то налетевший шар останавливается на месте, а шар, бывший в покое, откатывается со скоростью первого шара.

Очень интересно следить за тем, что происходит, когда шар налетает на цепь соприкасающихся шаров, расставленных прямой шеренгой. Удар, полученный крайним шаром, как бы проносится через цепь, но все шары остаются на своих местах, и только крайний шар, самый далекий от места удара, отлетает в сторону: ему нечему передать удар и получить его обратно.

Этот опыт можно проделать с крокетными шарами, но он хорошо удается и с шашками или с монетами. Расположите шашки в прямой ряд – можете и очень длинный, но так, чтобы они плотно примыкали одна к другой. Придержав пальцем крайнюю шашку, ударьте по ее ребру деревянной линейкой: вы увидите, как с другого конца отлетит крайняя шашка, а все промежуточные сохранят свои места.

Клоуны в цирках изумляют иногда публику тем, что сдергивают скатерть с накрытого стола, – но, к общему изумлению, все тарелки, стаканы, бутылки невредимо остаются на местах. Здесь нет ни чуда, ни обмана, – это дело ловкости, которая изощряется продолжительным упражнением.