Яков Перельман - Физика на каждом шагу

Пусть, например, нужно передвигать груз, требующий без шпиля усилия в 500 кг; имеется шпиль с валом радиуса 21 см и с водилами длиною 3 1/ 2м. Тогда усилие х, которое нужно приложить к концу водил, чтобы тащить груз, найдем из пропорции:

х: 500 = 21: 350,

откуда

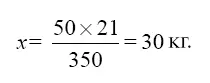
На вороте или на шпиле можно, значит, небольшою силою привести в движение значительный груз. Но скорость этого движения в таких случаях бывает невелика, – меньше, чем скорость, с какою движется приложенная к вороту сила.

Рассмотрим последний пример со шпилем: при одном полном обороте конец шеста, где приложена сила, описывает путь длиною

2 × 3,14 × 350 = 2200 см.

Тем временем вал сделает также один оборот, намотав на себя кусок веревки, длиною

2 × 3,14 × 21 = 130 см.

Следовательно, груз подтянется всего на 130 см. Сила прошла 2 200 см, а груз за то же время – только 130 см, т. е. почти в 17 раз меньше. Если сравните величину груза (500 кг) с величиною усилия, прилагаемого к шпилю (30 кг), то убедитесь, что между ними существует такое же отношение:

500: 30 = около 17.

Вы видите, что путь груза во столько же раз меньше пути силы, во сколько раз эта сила меньше груза. Другими словами: во сколько раз выигрывается в силе, во столько же раз теряется в скорости.

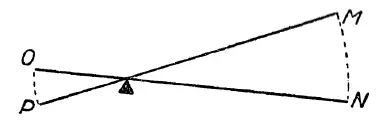
Рис. 17. Объяснение золотого правила механики

Это правило применимо не только к вороту или шпилю, но и к рычагу, и ко всякой вообще машине (его издавна называют «золотым правилом механики»).

Рассмотрим, например, рычаг, о котором говорилось на с. 51. Здесь выигрывается в силе в 3 раза, но зато, пока длинное плечо рычага (см. рис. 17) описывает своим концом большую дугу MN, конец короткого плеча описывает втрое меньшую дугу ОР. Следовательно, и в этом случае путь, проходимый грузом, меньше пути, проходимого в то же время силою, в 3 раза – во столько же раз, во сколько эта сила меньше груза.

Теперь вам станет понятно, почему в некоторых случаях выгодно пользоваться рычагами наоборот: действуя большою силой на короткое плечо, чтобы двигать маленький груз на конце длинного плеча. Какая выгода так поступать? Ведь мы теряем здесь в силе! Конечно, зато во столько же раз выигрываем в скорости. И когда нам необходима большая скорость, мы приобретаем ее этой ценой. Такие рычаги представляют кости наших рук (рис. 18): в них мускул прикреплен к короткому плечу рычага 2-го рода и приводит в быстрое движение кисть руки.

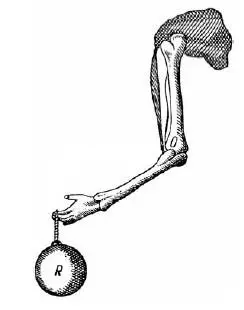
Рис. 18. Наша рука – рычаг. Какого рода?

В данном случае потеря силы вознаграждается выигрышем скорости. Мы были бы крайне медлительными существами, если бы кости нашего скелета были устроены как рычаги, выигрывающие в силе и, значит, теряющие в скорости.

Учение о рычаге разработано было впервые древнегреческим математиком Архимедом, жившим в Сиракузах (Сицилия) за двести лет до нашей эры. Легенды, в которых, вероятно, кроется большая доля истины, повествуют о замечательных машинах, которые были придуманы им на основе рычага. Вот что рассказывает об этом древний историк Плутарх:

«Марцел (римский полководец) приближался и по суше и морем. На суше войско шло под командою Аппия, а сам Марцел плыл во главе шестидесяти галер, о пяти рядах весел, со всякого рода метательными снарядами и оружием. Восемь судов, соединенных вместе, составляли род обширного помоста, на котором возвышалась стенобитная машина. Так плыл он к городу, доверяясь громадности и могуществу приспособлений и своей славе. Это однако не смутило Архимеда. Что все это значило в сравнении с его машинами?

«Однажды Архимед написал царю (сиракузскому) Гиерону, которому он был родственник и друг, что данною силой можно подвинуть какой угодно груз. Увлеченный жаром и силой доказательств, он прибавил, что если бы была другая земля, то, перейдя на нее, он сдвинул бы с места нашу. Удивленный Гиерон просил Архимеда осуществить задачу на практике и показать ему случай передвижения огромного груза малою силой. Архимед выбрал одну из царских галер; с великим трудом, работою многих рук, перевел ее на землю, посадил на нее много народу и нагрузил, как обычно. Сам же сел на некотором расстоянии; потом без усилия стал потихоньку двигать конец машины, состоявшей из блоков и веревок, и тянуть галеру, которая пошла, не качаясь, как если бы плыла по ровной поверхности моря. Царь, пораженный виденным и оценив могущество науки, пригласил Архимеда построить машины, пригодные для осады в случае ли нападения, или обороны.