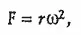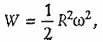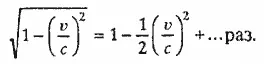Георгий Гамов - Приключения Мистера Томпкинса

Но для экспериментатора, находящегося внутри космического корабля, все выглядит иначе: яблоко «падает» с каким-то ускорением и, ударившись об пол, остается лежать на полу, придавленное к нему собственным весом. Бросая различные предметы, наш экспериментатор заметит, что все они падают с совершенно одинаковым ускорением (если пренебречь трением о воздух) и вспомнит, что это — закон свободного падения, открытый Галилео Галилеем. Но наш экспериментатор так и не сможет заметить ни малейшего различия между явлениями , происходящими в движущейся с ускорением кабине космического корабля и обычными явлениями гравитации. Он может пользоваться маятниковыми часами, ставить книги на полку, не боясь, что те улетят прочь, и повесить на гвоздь портрет Альберта Эйнштейна, который первым указал на эквивалентность ускорения системы отсчета и гравитации и на этой основе развил так называемую общую теорию относительности .

Но тут, как и в первом примере с вращающейся платформой, мы замечаем явления, оставшиеся неизвестными Галилею и Ньютону, когда те изучали гравитацию. Луч света, посланный через кабину, искривляется и освещает в зависимости от ускорения космического корабля каждый раз другое место экрана, висящего на противоположной стене. Разумеется, внешний наблюдатель интерпретирует это как суперпозицию равномерного прямолинейного движения света и ускоренного движения кабины, где производятся наблюдения. Геометрия также нарушается: сумма углов треугольника, образованного тремя лучами света, будет больше двух прямых углов, а отношение длины окружности к диаметру — больше числа пи. Мы рассмотрели лишь два из простейших примеров ускоренно движущихся систем отсчета, но установленная выше эквивалентность остается в силе для любого движения твердой или деформируемой системы отсчета.

Тут мы подходим к вопросу величайшей важности. Как мы только что видели, в ускоренно движущейся системе отсчета может наблюдаться ряд явлений, оставшихся неизвестными для обычного гравитационного поля. Существуют ли эти новые явления, такие как искривление луча света или замедление часов, и в гравитационных полях, порождаемых тяжелыми массами? Или, иначе говоря, существуют ли эффекты ускорения и эффекты гравитации, которые не только очень похожи, но и тождественны? Разумеется, ясно, что хотя с эвристической точки зрения весьма соблазнительно принять полное тождество этих двух разновидностей эффектов, окончательный ответ может быть дан только с помощью прямых экспериментов. И к величайшему удовлетворению нашего человеческого разума, требующего простоты и внутренней непротиворечивости законов Вселенной, эксперименты подтверждают существование новых явлений, о которых идет речь, и в обычном гравитационном поле. Разумеется, эффекты, предсказываемые гипотезой об эквивалентности полей ускорения и гравитационного поля, очень малы. Именно поэтому они и были открыты только после того, как ученые специально занялись их поиском.

Используя приведенный выше пример ускоренно движущихся систем отсчета, мы можем легко оценить два наиболее важных релятивистских гравитационных явления по порядку величины: изменение скорости хода часов и искривление луча света.

Рассмотрим сначала пример с вращающейся платформой. Из элементарной механики известно, что на частицу с единичной массой, расположенную на расстоянии r от центра, действует центробежная сила, вычисляемая по формуле

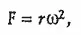
(1)

где омега — постоянная угловая скорость вращения нашей платформы.

Полная работа, совершаемая этой силой при движении частицы от центра до края платформы, равна величине

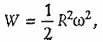
(2)

где R — радиус платформы.

Согласно сформулированному выше принципу эквивалентности мы должны отождествить центробежную силу F с силой тяжести на платформе, а работу W — с разностью значений гравитационного потенциала в центре и на краю платформы.

Напомним, что, как было показано в предыдущей лекции, часы, движущиеся со скоростью u, замедляют свой ход в

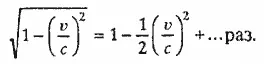
(3)

Если скорость u мала по сравнению со скоростью света с, то остальными членами можно пренебречь. По определению угловой скорости получаем r = R*омега, и «коэффициент замедления» можно представить в виде