Барри Паркер - Мечта Эйнштейна. В поисках единой теории строения

Немного изменив общую теорию относительности, Вейль построил теорию, которая описывала и электромагнитное и гравитационное поля. Удалось ли ему объединить их? Поначалу многие считали, что удалось, но детальный анализ показал, что теория несовершенна. Первым на её недостатки указал Эйнштейн.

Проблема заключалась в подходе к понятию длины. В теории относительности имеет смысл только длина в пространстве-времени. Другими словами, длина всегда включает в себя временну?ю часть, интервал времени. Это означает, что при движении двух одинаковых объектов разными путями к одной и той же точке, будет различна не только их длина, но и соответствующий временной интервал. Этот интервал может, например, соответствовать частоте колебаний атома. Отсюда следует, что два одинаковых атома, движущихся разными путями к одной точке, будут колебаться с разными частотами. Известно, что это не так, иначе мы не могли бы наблюдать чёткие спектральные линии в свете удалённых звёзд.

Вейль вскоре признал справедливость возражений и отказался от своей теории. Её можно было бы считать неудачей (на самом деле это не совсем так – подобная идея используется в современной теории поля), но благодаря ей удалось добиться важного результата – заинтересовать учёных возможностью объединения электромагнитного и гравитационного полей. Скоро над альтернативной теорией стали работать Эйнштейн и другие учёные.

В 1921 году ещё одну интересную попытку объединения предпринял немецкий учёный Теодор Калуца. Он показал, что если уравнения Эйнштейна записать не в четырёх, а в пяти измерениях, произойдёт то же чудо – в теории появятся уравнения Максвелла. Эйнштейн наверняка задавал себе вопрос: «Неужели господь подшучивает над нами?» Теперь кроме теории гравитационного поля Эйнштейна появились две других, и обе содержали уравнения электромагнитного поля – уравнения Максвелла. В течение нескольких лет учёные проявляли к теории Калуцы значительный интерес. Правда, оставалась нерешённой одна серьёзная проблема. В реальном мире только четыре измерения – три пространственных и одно временное. Что же это за пятое измерение? Где оно прячется? Калуца понимал, что требование соответствия реальному миру заставит его как-то избавиться от пятого измерения. Он сделал это при помощи приёма математической проекции, по аналогии с двумерной тенью трёхмерного объекта. Измерений стало столько же, сколько в реальном мире, но трудности не исчезли.

В 1926 году теорию дальше развил шведский физик Оскар Клейн. Он предположил, что пятое измерение физически не проявляется, поскольку имеет вид петли, столь туго затянутой, что её не видно. Другие учёные, в том числе Эйнштейн, стали разрабатывать эту теорию, но постепенно утратили к ней интерес. Дело в том, что из неё не следовало ничего нового. Она позволяла получить уравнения Максвелла и Эйнштейна, но не более того. Правда, в последнее время эта теория вновь привлекла к себе внимание, и некоторые учёные считают, что она в конце концов позволит добиться значительных успехов. Выдающийся физик-теоретик Абдус Салам недавно назвал её «одним из четырёх крупнейших достижений на пути к реализации мечты Эйнштейна». В последние годы значительный интерес вызвал современный вариант этой теории с 11 измерениями, связанный с другой важной теорией – супергравитацией. Об этом речь пойдёт дальше.

Ещё одна единая теория – геометродинамика – была предложена в 1957 году Мизнером и Уилером. Нужно отметить, что ту же идею высказал в 1925 году Райнах, но Мизнер с Уилером об этом не знали. Иногда её называют «уже объединённой теорией поля». Чтобы понять, почему, рассмотрим уравнения Эйнштейна, которые я раньше для простоты записал в виде A = B . Уилер и Мизнер обнаружили, что некоторыми манипуляциями можно привести A к такому же виду, как и B . При этом электромагнитное поле, которое раньше «пряталось» в B , становится таким же геометрическим членом, как и A . Уравнение в новой форме содержит и электромагнитное и гравитационное поля, но не имеет источников.

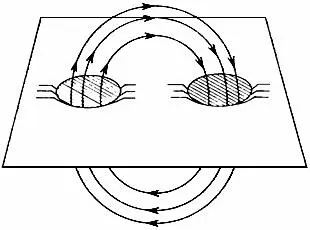
Упрощённое представление кротовой норы в пространстве. Силовые линии поля выходят из одной норы и уходят в другую

Может показаться, что уравнение без источников вызовет трудности. Откуда же тогда берутся оба поля? Мизнер и Уилер остроумно обошли эту трудность, использовав раннюю идею Эйнштейна – «кротовые норы» (Эйнштейн называл их мостиками в пространстве). Рассмотрим кротовые норы поближе. Линии поля входят в одну из них и выходят из другой. При взгляде сверху они кажутся источниками: один положительный – линии из него выходят, а другой отрицательный – линии в него входят. Но так как источниками электромагнитных и гравитационных полей являются частицы, то в их роли выступают кротовые норы. Получается, что вещества нет, есть только норы в пространстве, но это как раз то, чего хотел Эйнштейн. Он ненавидел сингулярности, а обычные источники – частицы – с неизбежностью их порождали. Кротовые норы позволяли обойти эту трудность.