Мичио Каку - Гиперпространство

А вот второй парадокс, связанный с воссозданием прошлого, представляет любопытные проблемы. Например, перемещаясь назад во времени, мы реализуем прошлое, а не разрушаем его. Таким образом, мировая линия изобретателя машины времени представляет собой замкнутую петлю. Его мировая линия скорее воспроизводит прошлое, нежели меняет его.

Гораздо запутаннее мировая линия Джейн — женщины, которая сама себе мать, отец, сын и дочь (рис. 11.2).

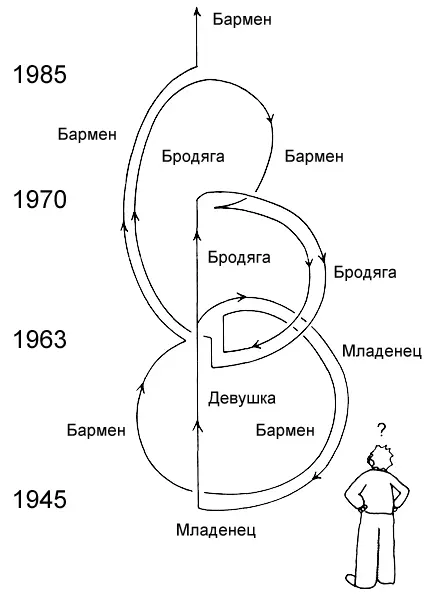
Рис. 11.2. Если путешествия во времени возможны, тогда наша мировая линия превращается в замкнутую петлю. В 1945 г. рождается девушка. В 1963 г. у нее появляется младенец. В 1970 г. она живет как бродяга, который возвращается в 1945 г., чтобы встретиться с самим собой. В 1985 г. он путешественник во времени, который знакомится с самим собой в баре в 1970 г., переносит себя назад в 1945 г., похищает младенца, доставляет его обратно в 1945 г., и все начинается заново. Эта девушка — ее собственная мать, отец, дед, бабушка, сын, дочь и т. д.

Еще раз отметим, что мы не в силах изменить прошлое. Когда наша мировая линия движется назад во времени, она просто реализует то, что уже известно. Следовательно, в такой вселенной вполне возможно встретить самого себя в прошлом. Прожив полностью один цикл, рано или поздно вы встретите юношу или девушку, которая окажется вами в молодости. Не удержавшись, вы скажете собеседнику, что его внешность подозрительно знакома вам. А потом вдруг вспомните, как однажды в молодости встретили странного человека постарше, который утверждал, что ваше лицо ему знакомо.

Таким образом, возможно, мы в состоянии выполнить прошлое, но не изменить его. Как мы уже указывали, мировые линии не прерываются и не кончаются. Вероятно, они могут образовывать петли во времени, но ни в коем случае не менять его.

Но схемы с линиями, похожими на световые конусы, представлены только в рамках специальной теории относительности, способной описать, что произойдет, если мы попадем в прошлое, однако слишком примитивной, чтобы разрешить вопрос о том, имеют ли они смысл. Для того чтобы ответить на этот более широкий вопрос, надо обратиться к общей теории относительности, где ситуация становится гораздо более щекотливой.

Благодаря теории относительности мы видим, что такие изогнутые мировые линии не противоречат законам физики. Эти замкнутые петли получили научное название замкнутых временеподобных кривых. В настоящее время в научных кругах ведутся споры о том, допустимы ли замкнутые временеподобные кривые в общей теории относительности и квантовой теории.

В 1949 г. Эйнштейна обеспокоило открытие одного из его близких друзей и коллег, венского математика Курта Гёделя из Института перспективных исследований в Принстоне, где работал и Эйнштейн. Гёдель нашел внушающее тревогу решение уравнений Эйнштейна, допускавшее нарушение основных принципов здравого смысла: его решение подразумевало определенные формы путешествий во времени. Впервые в истории идея путешествий во времени обрела математический фундамент.

В некоторых кругах Гёделя прозвали «спойлером» (от англ. spoiler — вредитель, пакостник). В 1931 г. он приобрел славу (сомнительную), доказав вопреки всем ожиданиям, что продемонстрировать самосогласованность арифметики нельзя. При этом он вдребезги разбил мечту двух тысячелетий, восходящую еще к временам Евклида и древних греков, которой полагалось увенчать достижения математиков: мечту о сведении всей математики к небольшому самосогласованному своду аксиом, из которых можно вывести все.

Проявив математическую ловкость, Гёдель доказал, что в арифметике всегда будут теоремы, корректность или некорректность которых невозможно продемонстрировать с помощью арифметических аксиом, т. е. арифметика всегда будет несовершенной. Результатом действий Гёделя стал, возможно, самый ошеломляющий и неожиданный поворот в развитии математической логики за целое тысячелетие.

Математика, некогда считавшаяся ввиду ее точности и определенности самой чистой из наук, не испорченной вульгарностью нашего материального мира, утратила свою определенность. После Гёделя стало казаться, что математика плывет по течению. (Грубо говоря, поразительное доказательство Гёделя помогло увидеть, что в логике присутствуют любопытные парадоксы. Возьмем, к примеру, утверждение «это высказывание ложно». Если высказывание истинно, значит, утверждение ложно. Если высказывание ложно, утверждение истинно. Или, например, если я сказал, что я лжец, тогда я лгу только в том случае, если говорю правду. Гёдель сформулировал утверждение «истинность этого высказывания не может быть доказана». Если утверждение корректно, значит, нельзя доказать, что оно корректно. Искусно сплетая замысловатую паутину подобных парадоксов, Гёдель показал, что существуют истинные утверждения, которые невозможно доказать арифметически.)