
Fig. 23.1. The gravitational force lines around the Sun.
String theory insists that gravity in the bulk is also described by force lines. If space in the bulk is not warped, then the Sun’s gravitational force lines will spread radially outward into the bulk (Figure 23.2). Because of the bulk’s extra dimension (just one in Interstellar ), there are three transverse dimensions into which gravity can spread instead of just two. Therefore, if the bulk exists and is not warped, then the density of force lines and thence gravity’s strength should decrease as 1/r 2when we move away from the Sun, rather than as 1/r 3. The sun’s pull on the Earth would be two hundred times weaker, and on Saturn 2000 times weaker. With gravity weakening so rapidly, the Sun couldn’t hold onto its planets; they would fly away into interstellar space.
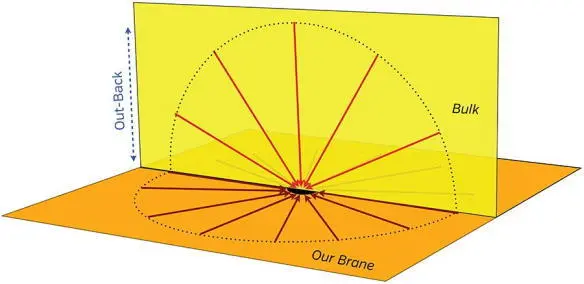
Fig. 23.2. Gravitational force lines spread radially into the bulk, if the bulk is not warped. The dotted circles are solely to guide your eyes. [Patterned on a figure in Lisa Randall’s Warped Passages (Randall 2006).]
But they don’t fly away. And their measured motions reveal unequivocally that the Sun’s gravity weakens as the inverse square of the distance. The conclusion is inescapable: if there is a bulk, it must be warped in some manner that prevents gravity from spreading into the fifth dimension, the out-back dimension.
Is Out-Back Curled Up?

If the bulk’s out-back dimension were curled up into a tight roll, then gravity could not spread far into the bulk, and the inverse square law would be restored.
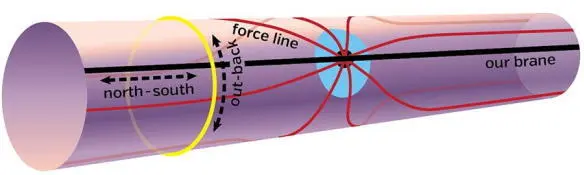
Fig. 23.3. If the out-back dimension ( yellow ) is curled up, then outside the blue circle a particle’s gravitational force lines ( red ) are parallel to our brane.
Figure 23.3 depicts this for the gravity of a tiny particle that resides at the center of the blue disk. In this picture, two space dimensions are suppressed, so we see only one of our brane’s dimensions (call it north-south) along with the bulk’s out-back dimension. Near the particle, inside the blue disk, the force lines spread in the out-back dimension as well as north-south, so (with the missing dimensions restored) gravity’s strength obeys an inverse cube law. However, outside the blue disk the curl-up makes the force lines lie parallel to our brane. They spread no further into out-back, and Newton’s inverse square law is restored.
Physicists who struggle to understand quantum gravity think this is the fate of all the extra dimensions except possibly one or two: they are curled up on microscopic scales, preventing gravity from spreading too fast. In Interstellar , Christopher Nolan ignores these curled-up dimensions and focuses on just one bulk dimension that’s not curled up. This becomes his out-back, fifth dimension.
Why should out-back not be curled up? For Chris the answer is simple: A curled-up bulk has very little volume—nowhere near enough volume to be an arena for interesting science fiction. For Cooper to travel into the bulk riding in the tesseract, as he does in the movie, the tesseract needs far more volume than a curled-up dimension would provide.
Out-Back: The Anti-DeSitter Warp

In 1999, Lisa Randall at Princeton University and MIT and Raman Sundrum at Boston University (Figure 23.4) conceived another way to stop gravitational force lines from spreading into the bulk: the bulk could suffer what is called “Anti-deSitter warping.” This warping might be produced by what are called “quantum fluctuations of bulk fields”—but that’s irrelevant to my story so I do not explain it here. [37] I discuss quantum fluctuations in Chapter 26 and bulk fields in Chapter 25.
Suffice it to say that this mechanism to produce the warping is very natural. By contrast, the Anti-deSitter (AdS) warping itself does not look natural at all. It looks downright weird.

Fig. 23.4. Lisa Randall (1962– , right) and Raman Sundrum (1964– , left).
Suppose you’re a microbe, and you live in a face of a microscopic tesseract (Chapter 29). You travel, in your tesseract, out from our brane; perpendicularly out (straight up in Figure 23.5). And suppose you have a microbial pal, who also travels perpendicularly out from our brane. When you and your pal depart our brane, you are 1 kilometer apart (1000 meters; about 0.6 miles). Although you both travel precisely outward, perpendicular to our brane, your separation plummets precipitously due to AdS warping. When you have traveled a tenth of a millimeter (the thickness of a human hair), your separation has decreased tenfold: from 1 kilometer to 100 meters. The next 0.1 millimeter of travel reduces your separation by another factor of ten, to 10 meters; the next 0.1 millimeter reduces it to 1 meter; and so forth.
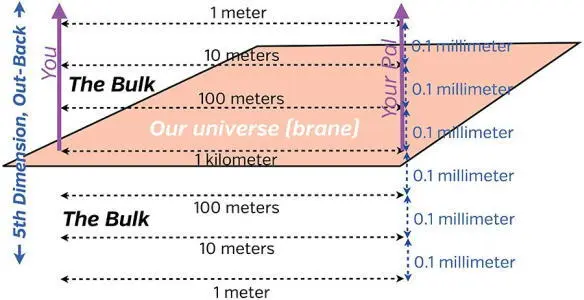
Fig. 23.5. AdS warping of the bulk.
This shrinkage of distances parallel to our brane is hard to imagine. I don’t know a good way to draw it, no better way than Figure 23.5. But it has marvelous consequences.
It has the potential to explain a mystery called the “hierarchy problem in the laws of physics”—but that’s outside the scope of this book. [38] For details see Lisa Randall’s Warped Passages (HarperCollins, 2006).
And because of the shrinkage, there is very little volume, above or below our brane, into which gravitational force lines can spread (Figure 23.6). Closer to our brane than 0.1 millimeter, the force lines spread into three transverse dimensions with impunity, so gravity obeys an inverse cube law. Farther than 0.1 millimeter, the force lines are bent parallel to our brane and so spread into just two transverse dimensions, whence gravity obeys the observed inverse square law. [39] Why is the magic distance, at which the inverse square law begins, 0.1 millimeter instead of, say, 1 kilometer or 1 picometer? I have chosen 0.1 millimeter quite arbitrarily. Experiments have proved that gravity obeys the inverse square law down to about 0.1 millimeter, so that is an upper limit on the magic distance. It could perfectly well be smaller.
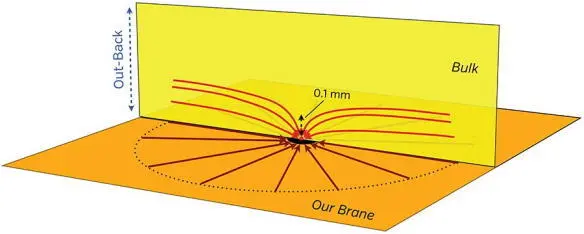
Fig. 23.6. If the bulk experiences AdS warping, then gravitational force lines bend parallel to our brane, because far from the brane there is very little volume in which to spread. [Patterned on a figure in Lisa Randall’s Warped Passages (Randall 2006).]
The AdS Sandwich: Plenty of Room in the Bulk
Читать дальше



















