Дэйв Голдберг - Вселенная в зеркале заднего вида. Был ли Бог правшой? Или скрытая симметрия, антивещество и бозон Хиггса

1. Для любых систем отсчета, для которых справедливы законы механики, справедливы и одни и те же законы электродинамики и оптики.

2. Свет всегда распространяется в пустом пространстве с определенной скоростью с, которая не зависит от состояния движения источника света.

Эйнштейн предположил, что во вселенной наличествует еще одна, причем очень важная симметрия. Что-то — скорость света и законы физики — остается инвариантом, даже когда наблюдатели движутся с разными скоростями. Эта симметрия не носит имени Эйнштейна, однако в ней суммированы его постулаты.

Лоренц-инвариантность.Физический закон записывается в таком виде, чтобы его результаты не зависели от ориентации и скорости системы.

В частности, первый постулат Эйнштейна означает, что все эксперименты должны приводить к одним и тем же результатам для наблюдателей, находящихся в инерциальных системах отсчета, — то есть всякого, кто в зависимости от вашей точки зрения находится в покое, либо движется с постоянной скоростью и никуда не сворачивает.

Внесу ясность и приведу несколько оговорок. Не всякому дано быть наблюдателем в инерциальной системе отсчета. Например, когда разгоняешь автомобиль, тебя вжимает в спинку сиденья — и прямо чувствуешь, что движешься не с постоянной скоростью. Специальная теория относительности потому и специальна, что полагается на наличие инерциальной системы отсчета.

Эйнштейн додумался до колоссальной идеи, симметрии, которой мы уже касались в контексте второго закона термодинамики: пространство и время совсем не так различны, как все раньше думали. В зависимости от того, как двигаешься, пространство и время с легкостью перемешиваются друг с другом. Мы еще не готовы заниматься искривлением пространства-времени, однако в качестве осознанной и продуманной разминки давайте рассмотрим идею, которая, как ни странно, с ним связана: повороты в обычном пространстве.

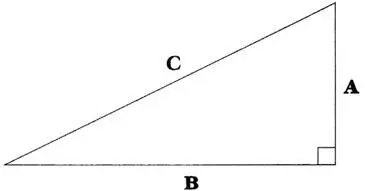
С теоремой Пифагора вы, несомненно, знакомы:

Это равенство обманчиво простое на вид. Переменные А и В — длины коротких сторон прямоугольного треугольника, а С — длина его большой стороны, гипотенузы.

Теорема Пифагора рассказывает нам отнюдь не только о быте и нравах треугольников как таковых. Она учит вычислять расстояние между точками. Наверное, подобные задачи вы помните еще со школьных лет: пройдите 3 километра на восток, потом 4 километра на север. Продеритесь через вычисления — и обнаружите, что вы в 5 километрах от начальной точки.

Чтобы связать это с реальной жизнью, рассмотрим маленький кусочек плана города Вашингтона.

Многие города удобно устроены так, что их улицы идут примерно в направлении основных сторон света. Вашингтон — идеальный тому пример: нумерованные улицы идут с севера на юг, а улицы с буквенными обозначениями — с востока на запад.

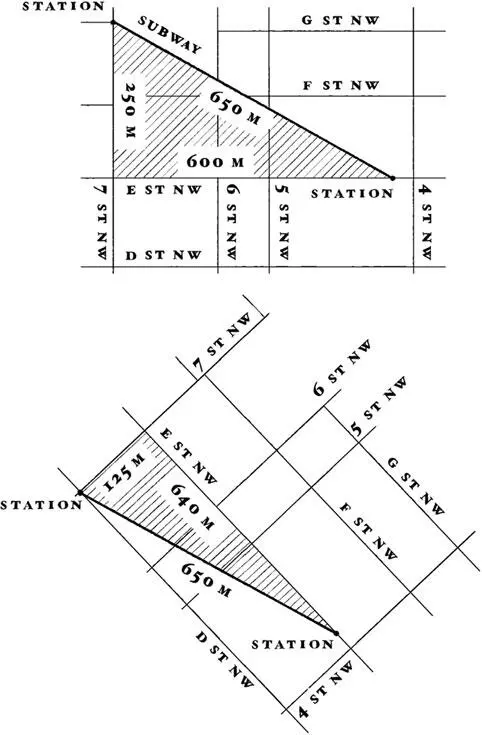
Итак, приведу пример, найденный в результате лихорадочных поисков в Google Maps . Если хочешь пройти от станции метро «Джудикери-север» на углу Четвертой и Е-стрит Северо-Западного квадранта до станции «Чайнатаун» на углу Седьмой и Джи-стрит, сначала надо пройти около 600 метров на запад по Е-стрит, а потом 250 метров на север по Седьмой.

Естественно, можно просто спуститься в метро и прокатиться по красной линии, и если проделать нужные вычисления, окажется, что продолжительность поездки составит около 650 метров. Вот вам практическое применение теоремы Пифагора, хотя мы слегка изменили названия переменных:

Подобной традицией мы обязаны трудам математика и философа XVII века Рене Декарта. Декартова система координат позволяет наносить все события и предметы во вселенной на своего рода карту. Например, место предмета по направлению с запада на восток принято обозначать буквой х . По направлению с юга на север мы обычно помечаем его положение как у . Возможностью перемещаться еще и по вертикали, скажем, на лифте, я пренебрегаю, но если у вас есть к этому тяга, можете назвать это направление движения z .

План Вашингтона

С моей стороны было бы преступным упущением не указать на то, что на поверхности Земли декартова система координат терпит полный крах. Земля-то круглая, а значит, создать идеальную, без искажений карту, которая покрывала ее целиком, невозможно [62] Реплика в сторону из серии «это интересно»: в 2007 году мы с Дж. Ричардом Готтом математически доказали, что наилучшее сочетание минимальных искажений достигается при картографической проекции под названием «Тройная проекция Винкеля». Очевидно, журнал « National Geographic » пришел к тому же выводу, потому что они уже больше десяти лет применяют тройную проекцию Винкеля для своих карт мира. . Ничего страшного, именно поэтому мы взяли для примера лишь крошечный фрагмент земной поверхности — несколько городских кварталов.